1) Якщо обидва операнди є додатні (рис. 1.9,б), то за умови (1.3) матимемо модуль суми
X=A+B=S<2n, (1.4,а)
а додавання знакових бітів як звичайних розрядів становить знак суми
Z=0+0=0, (1.5,а)
отже, дістанемо в підсумку правильний результат (знаковий біт відокремлено крапкою)
Z.X=0.S. (1.6,а)
За невиконання умови (1.3) в (1.4,а) отримаємо що означає перенесення до знакового розряду, тому (1.5,а) дасть Z=0+0+1=1, і в підсумку (1.6,а) матимемо Z.X=1.(2n-S)=1.Sдоп, тобто дістанемо від’ємну суму за додатних операндів. Це й буде індикувати переповнення розрядної сітки, що автоматично виконується мікропроцесором.
2) Якщо операнди мають різні знаки і додатний більший за модуль від’ємного (рис. 1.9,в), то, враховуючи, що модуль доповняльного коду від’ємного числа X2 визначається як 2n-|X2| і що число 2n дає одиницю перенесення c до знакового розряду, аналогічно (1.4,а...1.6,а) матимемо:
X=A+(2n-|B|)=(A-|B|)+2n=
=S +c>2n; (1.4,б)
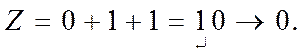 (1.5,б)
(1.5,б)
Отже, відкидаючи одиницю перенесення (показано відокремленням) зі знакового розряду, дістанемо правильний підсумок
Z.X=0.S. (1.6,б)
Те ж саме маємо під час додавання в оберненому коді, але в підсумку буде на 1 менше, тому згадане перенесення потрібно додати до суми, аби її
скоригувати (стрілка на рис. 1.9,в).
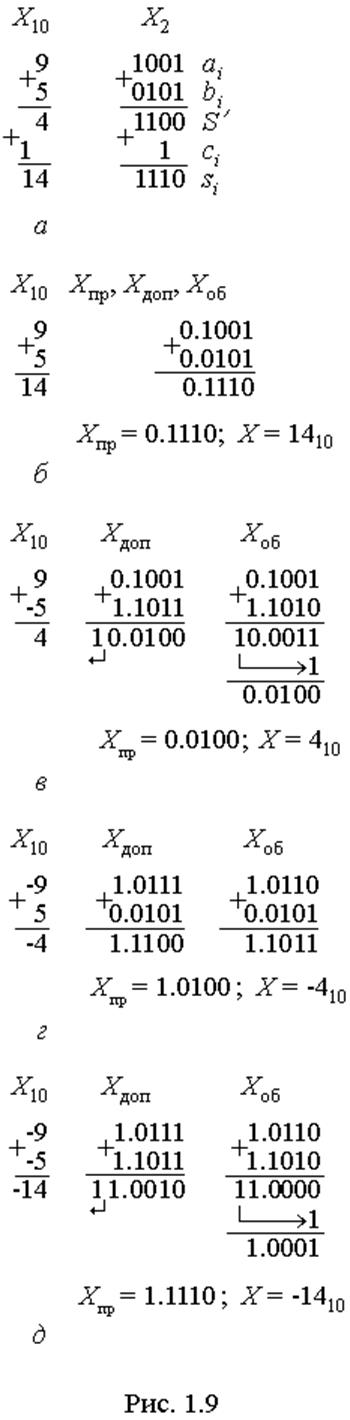 3) Якщо операнди різних знаків, але тепер
3) Якщо операнди різних знаків, але тепер
від’ємний за модулем більший, ніж додатний
(рис. 1.9,г), то
X=(2n-| A |)+B=2n-(| A | -B)=2n-| S |=Sдоп<2n; (1.4,в)
Z =1+0=1; (1.5,в)
Z.X=1.Sдоп, (1.6,в)
тобто дістанемо правильний результат у доповняльному коді. У цьому випадку, як і в попередньому (за різних знаків доданків), переповнення не утворюється, тому й немає потреби його контролювати.
4) Якщо обидва доданки від’ємні (рис. 1.9,д), то за умови (1.3) дістанемо
X=(2n-| A|)+(2n-|B|)=2n+[2n-(| A|+|B|)]=
=2n+(2n-| S|)=c+Sдоп>2n; (1.4,г)
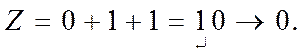 (1.5,г)
(1.5,г)
Z.X=1.Sдоп. (1.6,г)
Як і в другому випадку, відкидаючи перенесення зі знакового розряду під час додавання в доповняльному коді та додаючи його до суми під час додавання в оберненому коді, отримаємо правильний результат відповідно в доповняльному й оберненому кодах. Щодо контролю переповнення, воно виконується аналогічно першому випадкові.
Віднімання чисел зі знаком легко замінити їх додаванням, якщо від’ємник знов перетворити в доповняльний або обернений код. Наприклад, операція (-A)-(-B)=-A+B фактично повторює операцію додавання (див. рис. 1.9,г), тому розглянуті правила дійсні й для віднімання.
Отже, щодо додавання чисел з нерухомою комою в двійковій системі слід відзначити таке: 1) додавання чисел зі знаком зводиться до операції додавання в доповняльному або оберненому коді їх розрядів, включаючи знаковий; 2) якщо виникає перенесення в знаковому розряді суми, то під час виконання операції в доповняльному коді його відкидають, а в оберненому коді – додають до суми; 3) результат одержують у тому ж коді, в якому зображено операнди; 4) якщо доданки мають різні знаки, то переповнення не виникає, а якщо однакові, то знак суми збігається з їх знаком, в іншому разі індикується переповнення розрядної сітки; 5) у доповняльному коді не виникає потреби коригувати суму додаванням до неї одиниці перенесення знакового розряду, тому він використовується частіше; 6) віднімання чисел зі знаком, зображених у доповняльному або оберненому кодах, зводиться до їх додавання, якщо зменшуване залишити незмінним, а над від’ємником виконати операцію відповідно доповнення або обернення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.