Арифметичні основи цифрової техніки (Глава 1 навчального посібника)

Глава 1

АРИФМЕТИЧНІ ОСНОВИ ЦИФРОВОЇ ТЕХНІКИ

§1.1. ПЕРЕТВОРЕННЯ ЧИСЕЛ МІЖ СИСТЕМАМИ

ЧИСЛЕННЯ

1.1.1. Системи числення

У позиційній системі числення (СЧ), на відміну від непозиційної, наприклад, римської, кількість, позначувана цифрою хі, залежить від її позиції – розряду і в числі

                                Xc=xn-1xn-2...x1x0,x-1x-2...x-m,           (1.1)

де n, m - кількість цифр відповідно в цілій та дробовій частинах числа, відокремлюваних одна від однієї розділовою комою або крапкою. Найбільшого поширення набули позиційні СЧ, в яких вага розрядів сі (кількісне значення кожної їх одиниці) змінюється в геометричній прогресії, знаменник якої с є основою СЧ, що дорівнює кількості різних цифр, потрібних для запису довільного числа. Отже, запис (1.1) відповідає кількості

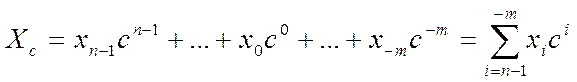                     ,               (1.2)

наприклад, 904,110=9·102+0·101+4·100+1·10-1.

У найуживаніших СЧ (табл.1.1) використовуються арабські цифри, а якщо їх бракує - також літери латинської абетки: цифри A,...,F відповідають десятковим числам 10,...,15. (Цифри можуть позначатися і від'ємними чис­лами, наприклад, у знакорозрядних формах двійкової і трійкової СЧ застосо­вуються цифри 1, 0, 1 , де 1= –1). Крім індексних уживаються також літерні позначення СЧ: D (Decimal), B (Binary), H (Hexadecimal), Q (Octal), наприк­лад, 94.1= 94,110= = 94.1D; 10,012= 10.01B; 7B,A16= 7B.AH; 76,58= 76.5Q.

У табл.1.2 наведено приклади на деякі числа в основних СЧ. Якщо числа в різних СЧ відповідають однаковій кількості, вони є еквівалентними, на­приклад, 10101100,12=254,48=172,510=AC,816; найдовшими  є двійкові числа, найкоротшими – шістнадцяткові, звичайно, зручнішими для людини – десят­кові.

                                                                                                      Таблиця 1.1

Як відомо, у цифровій техніці використовується переважно двійкова СЧ, бо їй властиві такі позитивні якості: найпростіша реалізація елемента для ві­дображення всього двох цифр; найбільша завадостійкість, зумовлена тим, що під час дії завад, дестабілізівних чинників тощо легше розрізнити два рівні напруги, ніж кілька; простота виконання арифметичних та логічних операцій і пов'язана з цим висока швидкодія; ощадливість та можливість уніфікації обладнання.

                                                                                              Таблиця 1.2

1.1.2. Перетворення між двійковою, шістнадцятковою та