Арифметичні основи цифрової техніки (Глава 1 навчального посібника), страница 5

Під час зображення малих чисел старші розряди витискаються нулями і коли молодші розряди не вміщуються в розрядній сітці, вони не сприймаються ЕОМ (тому число, менше за 2-m, називають машинним нулем), внаслідок чого виникає абсолютна похибка, що не перевищує одиниці молодшого розряду D=2-m. Звідси дістаємо відносну похибку в усьому діапазоні чисел

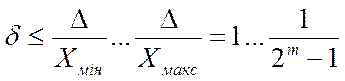
Наприклад, для однобайтового слова (n=8, m=7) маємо в діапазоні чисел              1/128...127/128 відносну похибку біля 100% ... 0,8 %, тобто, як і слід було сподіватися, малі числа зображаються з дуже великою похибкою.

    1.2.4. Форма зображення чисел з рухомою комою

У формі зображення з  рухомою (пливною) комою (рис. 1.5,д) число подається в показниковому (або півлогарифмічному: половина зображення показникова) вигляді:

X=M·2Е,

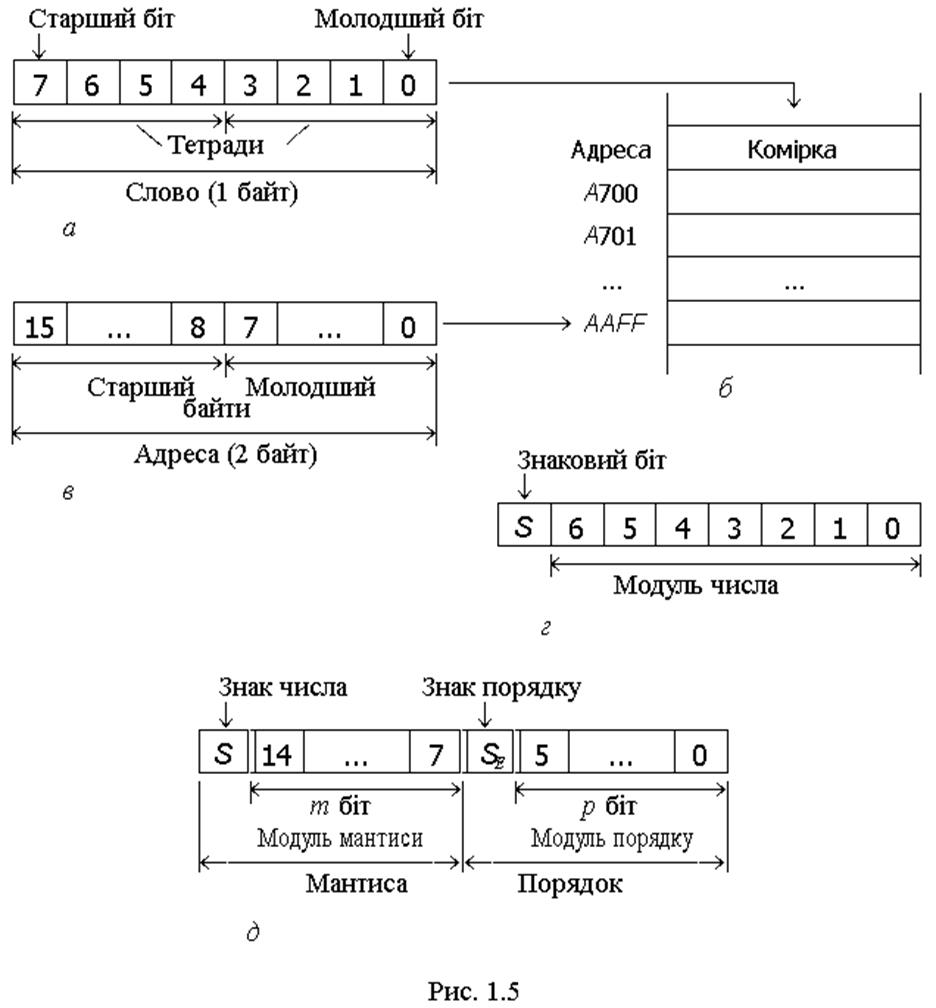
де M – мантиса, E – порядок числа; два біти приділено знакам: S  – знаковий біт числа, SЕ – знаковий біт порядку. Здебільшого, модуль мантиси сприймається як правильний дріб (уявна кома є між бітом S та старшим бітом мантиси), а модуль порядку – завжди як ціле число.

Наприклад, якщо в двобайтовому слові 2 біти приділено знакам,  8 біт – модулю мантиси та 6 біт – модулю порядку, то зображення 1.01010000.0.000100 (розділові крапки між частинами слова зазначено умовно) є число X=(-0,0101·2+100)2=-1012=-510. Таке зображення вважається ненормалізованим, проте частіше вживається нормалізоване, до якого переходять за допомогою перації нормалізацїї: мантиса зсувається ліворуч доти, поки з'явиться одиниця після знакового біта числа (кожний крок зсуву еквівалентний множенню на 2), а порядок числа, аби воно не змінилося, зменшується на кількість кроків зсуву (еквівалентно діленню по черзі на 2). У нашому прикладі один крок ліворуч дає нормалізоване зображення числа X=(-0,101·2+11)2=-1012=-510.

У нормалізованому числі найменше значення мантиси, відмінне від нуля, становить Mмiн=0,10...02=2-1, її найбільша величина Mмакс=0,11...12=1-2-m»1 та найбільше значення модуля порядку Eмакс=2p-1, де m, p – кількість розрядів у модулях відповідно мантиси та порядку. Звідси маємо модулі найменшого й найбільшого чисел

,

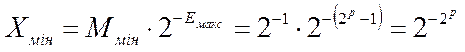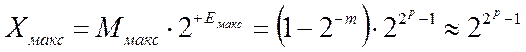
та діапазон їх зображення X=2-2p...22p-1, який у нашому прикладі при m=8, p=6 становить X=2-64...263.

Абсолютна похибка зображення мантиси, яка не перевищує =2-m, визначає відносну похибку зображення чисел у всьому їх діапазоні (тут порядок числа не враховуємо, бо він входить до чисельників та знаменників):

,

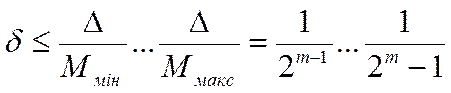тобто в нашому прикладі змінюється в діапазоні 2-7...2-8<0,8%...0,4%.

З метою розширення діапазону зображуваних чисел без збільшення довжини розрядної сітки в сучасних ЕОМ числа з рухомою комою подаються в шістнадцятковій системі числення

X=M·16E

з довжиною слова 4 байти (32 розряди) або зі збільшеною кількістю розрядів мантиси для підвищення точності у форматі слова 8 байтів (64 розряди).

Отже, інформаційну ємність цифрових пристроїв, каналів передачі даних оцінюють логарифмічною мірою кількості інформації в бітах і байтах, а кількість інформації, що зберігається в пам'яті ЕОМ, характеризують ємністю адресованої пам'яті.

Будь-яка інформація може зображатися в ЕОМ у формі слова (без знака) або цілого числа зі знаком, в останньому випадку 1 біт слова  займає знак. Дробові числа зображаються у формі з нерухомою та рухомою комою. Форма з рухомою комою дозволяє зображати числа в дуже широкому діапазоні з приблизно однаковою похибкою, яка визначається довжиною мантиси, але арифметичні операції ускладнюються тим, що їх потрібно виконувати окремо над мантисою і порядком. Тому ця форма вживається частіше в універсальних ЕОМ. Діапазон зображуваних чисел у формі з нерухомою комою значно вужчий і похибка подання малих чисел може неприпустимо збільшуватися. Проте застосуванням відповідних одиниць вимірювання фізичних величин та масштабуванням дані радіотехнічних пристроїв можна вписати до розрядної сітки таким чином, аби  уникнути великих похибок зображення. Простота виконання арифметичних дій і через це можливість підвищення швидкодії та ощадливість обладнання зумовили широке застосування форми зображення чисел з нерухомою комою в спеціалізованих, зокрема, радіотехнічних інформаційно-вимірювальних системах.