Цей алгоритм застосовується й для перетворення X10®X2, а з огляду на те, що двійкові вагові коефіцієнти дуже легко визначаються, це перетворення можна виконати послідовним відніманням (рис. 1.3,б) від десяткового числа (19,375) і кожної наступної різниці (3,375; 1,375; ...) найбільших вагових коефіцієнтів, що не перевищують зменшуваного (16<19,375; 2<3,375; ...). Лишається тільки записати одиниці до тих розрядів двійкового числа, що відповідають від'ємникам, а до решти розрядів – нулі. Кількість операцій у порівнянні з попереднім алгоритмом тут зменшується на кількість нулів у двійковому числі (наприклад, у перетворенні 102510®X2 зменшується на порядок). Проте великі десяткові числа швидше перетворити в двійкові за схемою X10®X16®X2 (рис. 1.3,в).
1.1.5. Деякі спрощення перетворень між системами числення
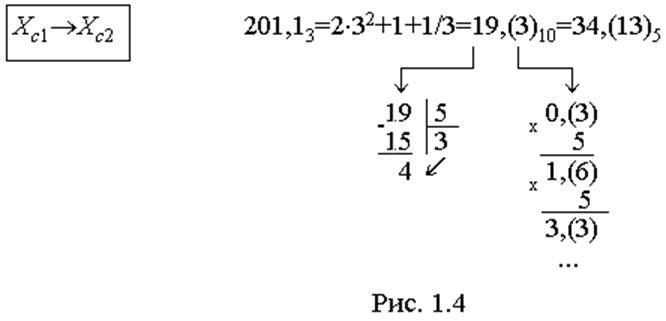
Звернімо увагу на те, що для перетворень між будь-якою системою та десятковою Xс®X10, ми користувалися алгоритмами, в яких арифметичні дії виконуються в десятковій системі. Якщо необхідно перетворювати числа між довільними системами Xс1®Xс2, крім випадку c2=c1k, то операції доводиться здійснювати в арифметиці довільної системи, що викликає незручності. Тому варто йти простим шляхом Xс1®X10®Xс2, коли всі дії можна виконувати десятковою арифметикою, як, наприклад, зроблено перетворення X3®X5 (рис. 1.4). В алгоритмах машинного перетворення, навпаки, зручніше виконувати арифметичні дії в двійковій системі, наприклад, шляхом послідовного ділення і множення на число 10102.
Враховуючи, що зсув розряду числа ліворуч або праворуч, еквівалентний відповідно множенню або діленню на основу системи, можна спростити деякі перетворення, користуючись співвідношеннями, наприклад, для двійкової системи (три крапки означають, що цифра повторюється в k розрядах пос-піль):
1...1=2k-1; 0,1...1=1-2-k; X0...0=X·2k; 0,0...0X=X·2-(k+n),
де n – кількість розрядів числа Х.
Приклади. 1) 11111,11112=(25-1)+(1-2-4)=31+15/16; 2) 111100101,1111001012 =
=(24-1) ·25+5+(1-2-4+5·2-9)=15·25+5+1-(25-5) ·2-9=485+(1-27/512)=485+485/512.
Як і слід було сподіватися, дробову частину можна перетворити як ціле число, а відтак помножити його на 2-m, де m – кількість розрядів після коми. Природно, аналогічно спрощуються перетворення і з інших систем до десят-кової. Наприклад, 1400.FF16=20·162+(1-16-2)=5120+255/256.
§1.2. ІНФОРМАЦІЙНА ЄМНІСТЬ ТА ФОРМИ ЗОБРАЖЕННЯ ДВІЙКОВИХ ЧИСЕЛ
1.2.1. Одиниці кількості цифрової інформації
Змінюючи всі можливі сполучення цифр xi в (1.2), одержимо (вважаючи для простоти m=0) набір цілих чисел, які можна зобразити n розрядами Xc=0...(cn-1), тобто разом K=cn різних чисел. Наприклад, 3 розряди десяткової системи утворюють 103 чисел X10=0,...,999. Так само діапазон зображуваних n розрядами двійкових чисел становить X2=0,...,(2n-1), а їх кількість K=2n удвічі більша за вагу старшого розряду 2n-1.
Чим більша розрядність цифрового пристрою n, тим менша ймовірність p(Xi)=1/K (для рівноймовірних подій) прийняття ним від джерела якогось конкретного повідомлення – одного з діапазону K зображуваних чисел – і тим більша кількість інформації (як міра невизначеностіповідомлення) у ньому міститься. У теорії інформації прийнята логарифмічна міра її кількості, що для рівноймовірних подій становить
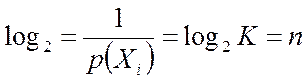
тобто визначається кількістю двійкових розрядів, яку вміщує той чи той пристрій.
Одиниця кількості двійкової інформації – біт (bit – binary digit – двійко-вий розряд; якщо використовуються десяткові логарифми, одиницею інфор-мації є діт, якщо натуральні – ніт) тлумачиться як така, що міститься в одно-му двійковому розряді, або як змінна xi, що може набувати тільки двох зна-чень: 0 та 1; 1 біт інформації можна відтворювати транзистором у ключовому режимі, передавати однодротовою лінією, зберігати в одному елементі пам'яті (тригері й т. ін.). Зростання інформаційної ємності (табл.1.3) потребує, природно, і збільшення обладнання. Так, для ємності 1 байт = 8 біт вже потрібна комірка пам'яті з восьми однобітових елементів і восьмидротова лінія, яка називається шиною даних.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.