2. Первое и второе соотношения для коэффициентов Эйнштейна, полученные на основе выражений для нагретого тела, не включают температуру. Следовательно, они справедливы для любого типа источника – являются универсальными.
3. Из второго соотношения следует, что при уменьшении длины волны отношение А21 / В21 возрастает. Отсюда следует, что при wν = const уменьшение λ сопровождается увеличением доли спонтанного излучения по сравнению с индуцированным. Рассмотрим причину этой закономерности. Если оставаться в рамках двухуровневой модели излучающей среды, то спад λ вызывает снижение энергии кванта εкв = W2 – W1 = hν = hc/ λ. Это эквивалентно повышению энергии верхнего уровня W2 при неизменном нижнем W1. С физической точки зрения рост энергии уровня усиливает неустойчивость возбужденной системы, стремящейся к состоянию с минимальной энергией. Неустойчивая возбужденная система релаксирует быстрее, время жизни на верхнем уровне t2 уменьшается, и, как следствие, растет количество спонтанных переходов А21 = 1/t2. Таким образом, при прочих равных условиях индуцированное излучение легче получить в длинноволновой области оптического диапазона, инфракрасной и видимой, и сложнее в УФ-области.
4. Используя
соотношения между коэффициентами Эйнштейна, можно выяснить, при какой
температуре среды вероятности (количества переходов в единицу времени) спонтанного
и индуцированного излучения выравниваются: А21 = wν В21. На основе (1.4) и (1.5)
перепишем условие равенства в другом виде:  . Для выполнения равенства вероятностей
экспонента должна равняться 2. Выбрав для примера переход с длиной волны
излучения λ = 1 мкм, получим, что температура среды должна быть порядка 4·104 К, что недостижимо в земных условиях.
Следовательно, на основе равновесной, нагретой среды реализовать оптическое
усиление и построить лазер не удастся.
. Для выполнения равенства вероятностей
экспонента должна равняться 2. Выбрав для примера переход с длиной волны
излучения λ = 1 мкм, получим, что температура среды должна быть порядка 4·104 К, что недостижимо в земных условиях.
Следовательно, на основе равновесной, нагретой среды реализовать оптическое
усиление и построить лазер не удастся.
5. Запишем выражение
для полной вероятности излучения одной частицы: ![]() и найдем А21 из второго соотношения:
и найдем А21 из второго соотношения:
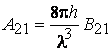 .
Тогда получим
.
Тогда получим 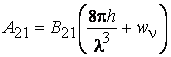 . Это означает, что если запрещено индуцированное излучение (коэффициент
Эйнштейна В21 = 0), то
. Это означает, что если запрещено индуцированное излучение (коэффициент
Эйнштейна В21 = 0), то ![]() 0, а следовательно, А21 = 0, т. е. запрещено и спонтанное
излучение. Выразив В21 через А21 и поставив выражение в
0, а следовательно, А21 = 0, т. е. запрещено и спонтанное
излучение. Выразив В21 через А21 и поставив выражение в ![]() , получим аналогичный результат: если
запрещено спонтанное излучение, то запрещено и индуцированное излучение. Эти
выводы подтверждают неразрывную связь всех видов оптических переходов.
, получим аналогичный результат: если
запрещено спонтанное излучение, то запрещено и индуцированное излучение. Эти
выводы подтверждают неразрывную связь всех видов оптических переходов.
1.4. Ширина и форма линий излучения
Все изложенное в 1.3 относилось к оптическим переходам, происходящим на фиксированной длине волны (частоте). Практика показывает, что реальные линии излучения и поглощения имеют конечную ширину. Рассмотрим причины этих явлений.
1.4.1. Естественная ширина и форма линий излучения
При естественных условиях
частицы изолированы друг от друга, отсутствуют взаимодействия с другими
частицами ансамбля. В основе получения выражения для естественной ширины
спектральной линии лежит соотношение Гейзенберга или принцип неопределенности,
который можно сформулировать следующим образом. Импульс p = mυ движущейся со скоростью υ частицы и ее координата х = υt не могут быть определены одновременно
с точностью, превышающей некую малую постоянную величину – приведенную
постоянную Планка ![]() . Соотношение Гейзенберга записывается
в виде:
. Соотношение Гейзенберга записывается
в виде: ![]() . Дифференциалы (неопределенности)
импульса и координаты, соответственно, равны dp = mdυ и dx = υdt. Учтем эти выражения и перепишем соотношение Гейзенберга
в другой форме:
. Дифференциалы (неопределенности)
импульса и координаты, соответственно, равны dp = mdυ и dx = υdt. Учтем эти выражения и перепишем соотношение Гейзенберга
в другой форме:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.