Оптическое излучение, страница 12

g(υ) =  (υ₀)^–1 exp [– (υ/υ₀)²],

где υ₀ – средняя наиболее вероятная скорость; m_p – масса протона; А – атомный номер.

С учетом допущений и введения обозначения  (ν₀υ₀ )/с получим:

g(ν)_нд = с(ν₀υ₀)^–1 exp {– [с(ν – ν₀)/(ν₀υ₀)]²} =

= (Δν_Т )^–1 exp {– [(ν – ν₀)/Δν_Т]²}.                             (1.11)

При ν = ν₀ форм-фактор g(ν)_нд  = g_max = 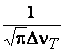. Если , то g(ν)_нд  = g_max /е, т. е. Δν_Т  – это ширина спектральной линии, соответствующая спаду g(ν)_нд  в е раз. Удобнее пользоваться шириной спектральной линии, измеренной на половинном уровне g_max. Поэтому вводят понятие доплеровской ширины линии Δν_д (рис. 1.24).

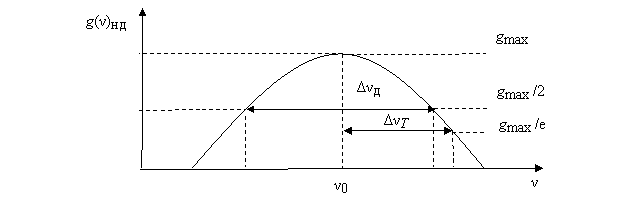
     Рис. 1.24. Контур неоднородно уширенной линии

Найдем связь между Δν_д  и Δν_Т . При ν – ν₀ = Δν_д /2  по определению g(ν)_нд  = g_max /2, а значит экспонента в (1.11) должна равняться 0,5 и тогда можно получить 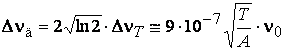 . В реальных условиях факторы, приводящие к однородному или неоднородному уширению, действуют на частицы одновременно. В конкретных условиях итоговый результат зависит от превалирования того или иного типа уширения. Так, например, в газовой среде гелий-неонового лазера для перехода с длиной волны 633 нм доплеровская ширина линии намного превышает Δν_одн, и уширение в целом носит неоднородный характер. Для инфракрасного перехода с   λ = 3391 нм значения Δν_д и Δν_одн  близки, что соответствует однородному уширению спектральной линии.

1.4.4. Дифференциальные и интегральные коэффициенты Эйнштейна

Функция спектральной плотности мощности любой однородно или неоднородно уширенной линии излучения полностью описывается соответствующим форм-фактором и амплитудой I₀ линии   . Система, содержащая множество частиц, по-разному излучает на разных частотах, следовательно, количество переходов (вероятности излучения по Эйнштейну) на этих частотах различны. Тогда коэффициент, характеризующий спонтанное излучение частицы, должен быть различным для отличающихся частот, т. е. частотно-зависимым: . Коэффициент  называют дифференциальным  коэффициентом Эйнштейна для спонтанного излучения частицы. Но если спонтанное излучение – частотно-зависимый процесс, а спектральная линия описывается форм-фактором  g(ν), то должно выполняться соотношение  .  Общее количество спонтанных переходов частицы известно: 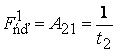, и оно должно равняться суммарному, интегральному количеству переходов на всех частотах в пределах спектральной линии:

                     ,                 (1.12)