Оптическое излучение, страница 7

         Для описания индуцированного излучения Эйнштейн ввел коэффициент В₂₁.  Поскольку речь идет об индуцированных процессах, вызываемых внешними квантами, то вероятность по Эйнштейну индуцированного излучения одной частицы (количество индуцированных квантов, формируемых в единицу времени) пропорциональна объемной спектральной плотности энергии  [c^–1].

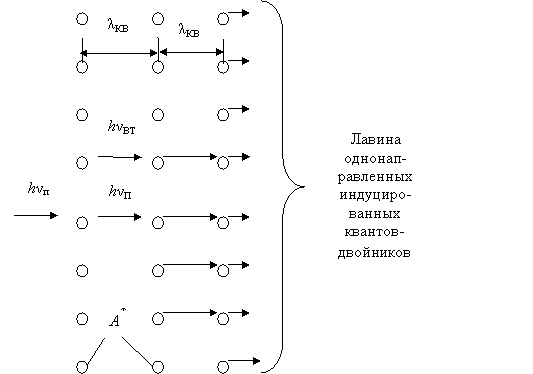
Рис. 1.17. Формирование потока индуцированных квантов

         Действуя аналогично случаю спонтанного излучения, при концентрации возбужденных частиц в равной n₂(А^*), для количества индуцированных переходов в единице объема можно записать 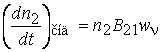  [м^–3 · с^–1].  Тогда для мощности индуцированного излучения системы объемом V и фиксированной энергией квантов hν запишем

 [Дж  · с^–1; Вт].

1.3.3. Вынужденное поглощение

         Внешний квант может взаимодействовать не только с возбужденной частицей, но и частицей, находящейся на нижнем энергетическом уровне. В результате вынужденного поглощения квант с энергией hν = W₂ – W₁ захватывается невозбужденной частицей (А), которая переходит после этого в возбужденное состояние А* (рис. 1.18). Для описания индуцированного поглощения Эйнштейн ввел коэффициент В₁₂. По Эйнштейну, вероятность индуцированного поглощения частицы (количество индуцированных квантов, поглощаемых частицей в единицу времени), как и вероятность индуцированного излучения, пропорциональна объемной спектральной плотности энергии  [c^–1]. Тогда количество актов индуцированного поглощения в единице объема системы с концентрацией частиц в нижнем энергетическом состоянии n₁(А) определится как 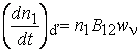     [м^–3 · с^–1]. 

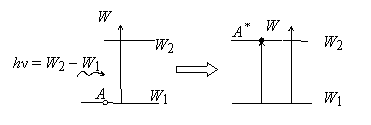
Рис. 1.18. Процесс вынужденного поглощения

Соответственно, частицы, находящиеся на нижнем энергетическом уровне системы объемом V  (в состоянии А), поглощают мощность .

1.3.4. Связь между коэффициентами Эйнштейна

             Процессы излучения и поглощения квантов в системе изменяют концентрации частиц на энергетических уровнях и, следовательно, влияют друг на друга. Для установления связи между введенными коэффициентами А₂₁, В₂₁ и В₁₂ Эйнштейн рассматривал простейшую двухуровневую  систему, находящуюся в термодинамическом равновесии (ТДР) с окружающей средой. При ТДР для концентраций частиц на энергетических уровнях W_i справедливо распределение Больцмана

,

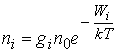где g_i – коэффициент вырождения – целое число, показывающее какое количество энергетических уровней с одинаковой энергией, но разными наборами квантовых чисел  (n, m l, s)  может находиться в системе. В условиях ТДР температура среды  Т = const, а подводимая  и отводимая энергии равны. Если говорить об излучающей системе, то в равновесном состоянии концентрации частиц на энергетических уровнях должны быть неизменны во времени: n₁, n₂ = const (t). Это условие требует, чтобы скорости изменения концентрации были нулевыми: . Следовательно, при ТДР в излучающей системе оптические переходы сверху вниз (2 → 1) должны уравновешиваться переходами снизу вверх (1 → 2). Иными словами, излучение квантов должно уравновешиваться их поглощением: Р_сп + Р_инд = Р_п. Воспользовавшись выражениями для мощностей из 1.3.1–1.3.3 и сократив общие сомножители, для равновесной излучающей системы получим: .  Отсюда для спектральной плотности энергии