Оптическое излучение, страница 11

Рис. 1.21. Однородное уширение спектральной линии

Форма однородно уширенной линии совпадает с формой естественной линии и  описывается функцией Лоренца при замене Δν_е  на Δν_одн:

.

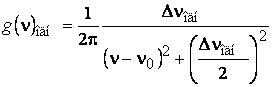К однородному уширению приводят факторы, которые одинаково воздействуют на весь ансамбль частиц. Внешние воздействия увеличивают количество переходов сверху вниз, т. е. сокращают время жизни частицы по сравнению с радиационным временем. К таким факторам относятся:

– спонтанное излучение с частотой переходов ;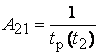

– индуцированное излучение с частотой переходов ;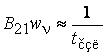

– столкновительные процессы между частицами в газах или в жидкостях, усиливающиеся, например, с ростом температуры и давления газа, и вызывающие переходы возбужденных частиц вниз с частотой ;

– воздействие внешних электрических и магнитных полей, вызывающих дополнительные девозбуждающие переходы:  и .

Общее количество оптических переходов при однородном уширении определится как 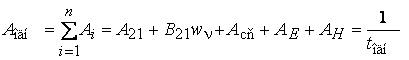   . В итоге А_одн >А_е, а t_одн < t_е. Однородные процессы сокращают время жизни частиц и увеличивают ширину линии излучения так, что Δν_одн > Δν_е.

1.4.3. Неоднородное уширение линии излучения

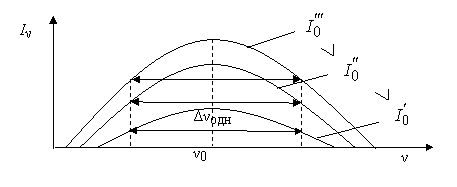
При неоднородном характере уширения форма и ширина спектральных линий отдельных частиц и ансамбля частиц не совпадают. Типичный для неоднородного уширения фактор – эффект Доплера. Для наблюдателя частота излучающих частиц будет зависеть от их скорости υ и направления движения:  ν = ν₀(1 + υ/с), причем скорость может быть больше или меньше нуля, а частоты больше или меньше ν₀ (рис. 1.22).

                                                I(ν)_нд

                                                              ν₀                                             ν

Рис. 1.22. Неоднородное уширение спектральных линий

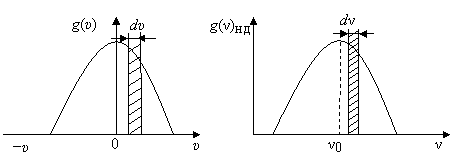
Ансамблю движущихся частиц соответствует пространство скоростей, которое можно описать функцией g(υ). В ансамбле всегда можно выделить группы частиц, имеющих примерно одинаковые скорости в интервале dυ. Каждому интервалу dυ в пространстве скоростей соответствует определенный интервал dν  в пространстве частот, описываемом  форм-фактором неоднородного уширения g(ν)_нд  (рис. 1.23, а, б).

                                                а                                                         б

Рис. 1.23. Пространства: а  – скоростей; б – частот

С учетом энергетических представлений  соответствие  интервалов может быть записано в виде g(ν)_ндdν = g(υ)dυ или g(ν)_нд = g(υ)dυ/dν. Из функции Доплера υ = (ν – ν₀) с /ν₀, что после дифференцирования дает  dυ или  dυ/dν = с/υ₀  и, соответственно, для форм-фактора неоднородно уширенной линии g(ν)_нд = g(υ)с/υ₀. Предположим, что распределение частиц по скоростям является максвелловским: