Лекция № 1, основные понятия, структурная схема систем передачи данных (СПД), страница 30

| D(t)| £ | l’_max(t)| Dt.

Оцененная т.о максимальная погрешность интерполяции может превышать действительную, но, тем не менее, такая оценка может быть полезна для приближенного определения шага квантования по времени по заданной максимальной погрешности.

Во многих случаях, когда возможность определения l’_max(t) отсутствует, пользуются частотным представлением контролируемого процесса. Согласно неравенству С. Н. Бернштейна для случайной функции имеющей спектральную плотность  с конечной частотой среза w_с=2p f_c:

| l^(k)_max(t)| £ w ^k_c| l_max(t)|  ,

где k - порядок производной. Для первой производной:

| l’_max(t)| £ w _c| l_max(t)|  , поэтому:

| D(t)| £ w_c Dt| l_max(t)|  . Т. е достаточно знать  частоту среза w_с  и максимальное значение функции на участке квантования l_max(t).

Для оценки погрешности линейной интерполяции воспользуемся интерполяционной формулой Ньютона.

l_k(t)=l(kDt)+ c_k(t - kDt)+R(t),

где 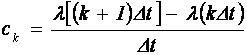 , R(t) – остаточный член, соответствующий погрешности интерполяции:

R(t)=0.5{ l²_k(t) (t-kDt) [ t - (k+1)Dt] }

Заменим l²(t) максимальным значением второй производной в данном интервале квантования:

| D(t)|=0.5{ l²_мах(t) (t - kDt) [ t - (k+1)Dt] }.