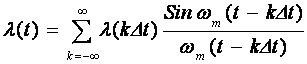 ,
,
который называют интерполяционный ряд Котельникова.
Т.о процесс восстановления l(t) можно рассматривать как суммирование откликов на бесконечную последовательность дискретных отсчетов l(kDt).
Имеется ряд затруднений использования результатов этой теоремы на практике. Во-первых, спектр реальных сигналов либо неограничен, либо слишком широк. В этом случае спектр сигнала ограничивают и вместо fmax выбирают частоту среза fc (обычно с учетом полной энергии, сосредоточенной в ограниченном fc спектре сигнала). Во-вторых, при использовании ряда Котельникова необходимо учитывать сумму бесконечной последовательности отсчетов. Поэтому ограничивают сумму отсчетов из соображения времени запаздывания восстановления. В-третьих, ВАХ реального ФНЧ отличается от идеального. Все это приводит к погрешностям восстановления сигнала. Чаще всего на приемной стороне восстанавливают дискретный сигнал с помощью ступенчатой интерполяций, реже – линейной и наиболее редко методом фильтрации по Котельникову и полиномами порядка выше первого.
Рассмотрим способы восстановления сообщения с помощью ступенчатой (полином нулевого порядка) и линейной (полином второго порядка) интерполяций. При ступенчатой интерполяции в каждом интервале Dt воспроизводится значением дискретного отсчета в начале интервала и сохраняется постоянным в течение всего интервала. Погрешность увеличивается, достигая наибольшего значения в конце интервала. При линейной интерполяции восстанавливаемое сообщение в интервале между отсчетами воспроизводится отрезком, соединяющим узлы интерполяции.
Точность минимальна при ступенчатой интерполяции и возрастает с увеличением степени интерполирующего полинома. Поэтому при одинаковой заданной точности восстановления, частота отсчетов для полиномов меньшего порядка должна быть выше. Оценим точность этих способов.
l(t)2=l(t)1+l’(t)(t2 - t1) где:D(t)=l’(t)(kDt - t), kDt£ t £ t, значит,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.