Основы теории рентгенографических исследований. Физические принципы рентгеноструктурного анализа глобулярных белков (Разделы 1-2 учебного пособия "Рентгенография биологических объектов"), страница 7

где  – интенсивность первичного пучка,  – заряд и масса электрона соответственно,  – скорость света,  – расстояние от образца до фотопленки. Обычно исключают все множители в (2.11) и выражают интенсивность по отношению к интенсивности рассеяния одним электроном. Тогда интенсивность рефлекса будет просто

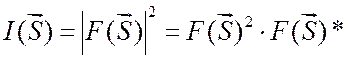                                  ,                     (2.12) где  – величина, комплексно сопряженная с .

Как было отмечено ранее, интегралы (1.8) и (1.9), определяющие амплитуду рассеяния, являются интегралами Фурье:

                      ,      

.

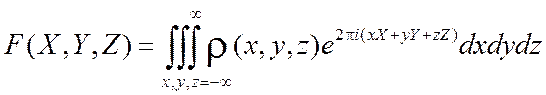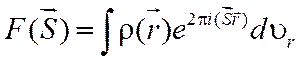Эти интегралы обладают свойством обратимости, состоящим в том, что по известной функции  можно вычислить электронную плотность с помощью обратного преобразования Фурье:

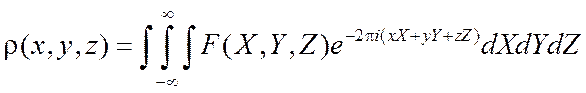                     (2.13)

или

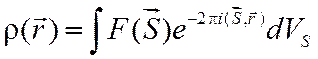                                        .                     (2.14)

Отличие обратного преобразования заключается в том, что показатель экспоненты имеет отрицательный знак. Выражения (2.13) и (2.14) служат для решения основной задачи дифракционных методов, которая заключается в определении электронной плотности  на основе регистрируемых дифракционных картин. Из эксперимента получают только модули структурных амплитуд, так как 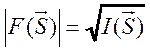. Но амплитуда  является комплексной величиной и характеризуется фазой .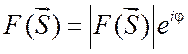

Следовательно, не зная фазы, нельзя рассчитать соответствующие интегралы и тем самым установить структуру белковой молекулы (фазовая проблема).

При рассмотрении интегралов Фурье вводят также понятие трансформанты Фурье. Так, например,  называют трансформантой Фурье от , а в свою очередь в силу свойства обратимости интегралов Фурье  является трансформантой (обратной) Фурье от . Поэтому  и являются парой трансформант.

Из соотношений (1.8) и (1.9) для амплитуды рассеяния вытекает, что

                                           .                                     (2.15)

Выражение (2.15) получается в силу того, что электронная плотность  является действительной функцией (за исключением случая аномального рассеяния). Соотношение (2.15) означает, что в центросимметричных точках обратного пространства амплитуды рассеяния равны по модулю 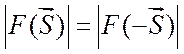 и противоположны по фазе (теорема Фриделя). Поэтому по виду дифракционной картины нельзя сказать, является ли объект центросимметричным, так как распределение интенсивностей, определяемое , всегда центросимметрично.

В случае кристаллов является периодической функцией. Поэтому вместо интеграла (26) используют ряд Фурье

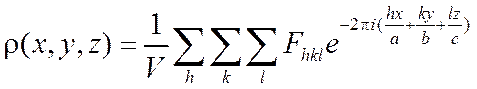                     .                  (2.16)

Таким образом, нахождение  сводится к расчету рядов Фурье с использованием полученных в эксперименте интенсивностей дифракционных максимумов. Здесь, конечно, необходимо знание фаз, и этот момент мы обсудим.

Существует следующее истолкование результатов рентгеноструктурного анализа, полученных расчетным путем. Например, проводят аналогию с образованием изображения в оптическом или электронном микроскопах. Процесс получения изображения можно разбить на два этапа. На первом этапе происходит рассеяние волн объектом. Этот этап такой же, как и рассеяние рентгеновских лучей объектом, – разложение Фурье (регистрация рентгенограмм). На втором этапе с помощью линз из рассеянных пучков получают изображение, то есть осуществляется синтез Фурье. Из-за отсутствия линз для рентгеновских лучей получение изображения достигается с помощью вычислений. Поэтому синтез Фурье по опытным данным можно рассматривать как «математический рентгеновский микроскоп», имеющий увеличение около 10⁸ раз.

Успехи рентгеноструктурного анализа белков, естественно, были связаны с решением фазовой проблемы. Это удалось сделать в середине 50-х годов ХХ века (М.Перутц и сотрудники, Англия), когда для исследования белка гемоглобина был применен так называемый метод тяжелоатомных производных. Прежде чем кратко ознакомиться с ним, вернемся еще раз к кристаллам белков. Один из принципиальных вопросов рентгенографического изучения белков, который в свое время длительно обсуждался, заключается в том, совпадает ли конформация молекулы белка в кристалле с ее структурой в водном растворе, являющейся функциональной, и не является ли эта структура результатом процесса кристаллизации. Если указанные структуры не совпадают, то это обесценивает результаты рентгеноструктурного анализа. Поэтому были проделаны многочисленные работы по сопоставлению структур белковых молекул в кристаллах и в растворах. В результате этого получены убедительные доказательства того, что конформации этих молекул в кристаллах подобны конформациям этих молекул в растворах (например, совпадают степени спиральности в молекулах белка, определенные рентгенографическим методом и оптическими измерениями в растворе). Сверх того показано, что ферментативная активность белковой глобулы в кристалле сохраняется, то есть он является биологически функциональным, что, по-видимому, есть следствие большого содержания воды в кристаллах.

Таким образом, в белковых кристаллах присутствуют пустоты, которые заполнены растворителем. Очевидно, что размеры этих пустот увеличиваются с увеличением размеров белковых макромолекул. Отметим, что такая структура кристалла требует изучения этих объектов во влажном состоянии, что и делается на практике. Обычно кристаллы белков с раствором помещают в тонкостенные запаянные капилляры.

В тяжелоатомной производной кристалла конформация белка должна оставаться такой же, как и в нативной структуре белка. Поэтому данный метод также еще называют методом изоморфного замещения. Изоморфное производное считают совершенным, если его распределение электронной плотности отличается от распределения электронной плотности нативного белка только наличием пика в положении замещения тяжелым атомом. Можно отметить, что в случае белка тяжелоатомные производные получаются путем изоморфного присоединения, а не замещения, так что, как предполагается, тяжелый атом замещает неупорядоченные молекулы растворителя, находящегося в указанных выше пустотах или каналах белкового кристалла.