Основы теории рентгенографических исследований. Физические принципы рентгеноструктурного анализа глобулярных белков (Разделы 1-2 учебного пособия "Рентгенография биологических объектов"), страница 2

                                  .                                                (1.1)

Это известная формула Брэггов-Вульфа, в которой угол θ (угол скольжения) есть угол между направлением падающего луча и кристаллической плоскостью, а n называют порядком отражения. Формула (1.1), полученная на основе геометрического вывода, дает правильный результат и используется для расчета межплоскостных расстояний. Однако она не раскрывает физической сущности явления дифракции. Поэтому при строгом рассмотрении дифракции необходимо учитывать вторичные волны, исходящие из всех точек объекта.

Рассмотрим задачу о рассеянии в общем виде для простого случая, когда рассеивающая система состоит из двух центров (рис. 1.1). Если на эти центры падает плоская волна, то она возбуждает их электроны, а сами центры становятся источниками вторичных волн. Как было сказано выше, дифракция происходит в том случае, когда длина волны λ по величине сопоставима с межатомными расстояниями . Если же , то разности фаз в любых направлениях практически не возникает и интенсивность рассеяния не зависит от угла. Обычно при исследовании биологических объектов используют  – излучение меди с λ=1,54 Å.

Рис. 1.1. Схема рассеяния на двух центрах

Пусть напряженность электрического поля падающей волны будет

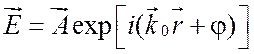                                                  ,                                (1.2)

где  – амплитуда волны, φ – начальная фаза. Укажем, что в формуле (1.2) отсутствует время, так как нас интересует не процесс распространения волны, а ее мгновенная картина в некоторый момент. Это связано с тем, что фазовые сдвиги рассеянных и интерферирующих между собой волн зависят лишь от геометрии волн и объекта и постоянны во времени.

Если выбрать начало координат в одном из рассеивающих центров, то положение второго определится радиусом-вектором , а разность хода волн, рассеянных двумя центрами, будет равна

,

где введен вектор

                                                   ,                                         (1.3)

играющий важную роль в теории дифракции. Кроме этого вектора, также используют вектор

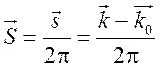                                    .                                                 (1.4)

Если падающая волна имеет единичную амплитуду (А=1), то рассеивающий центр в положении, определяемом вектором , дает волну

                                       ,                                           (1.5)

где f – рассеивающая сила центра, зависящая от его электронной плотности.

Из рис. 1.1 следует, что

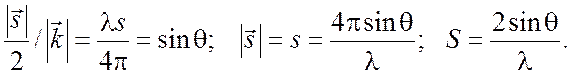                          (1.6)

Для нахождения результирующей волны в случае если объект содержит n рассеивающих центров, надо просуммировать выражения типа (1.5):

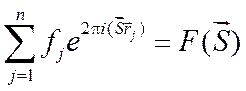                                      ,                                    (1.7)

где величина  называется структурной амплитудой рассеяния. Выражение (1.7) имеет универсальный характер, если под  понимать любую рассеивающую структуру. Это может быть электрон, атом, молекула, группа молекул и т.п.

В случае непрерывного распределения рассеивающих центров со средней по времени электронной плотностью системы сумма (1.7) заменяется интегралом типа интеграла Фурье

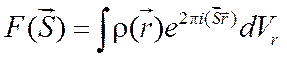                                        ,                        (1.8)

где  – элемент рассеивающего объема. Амплитуда рассеяния является функцией векторов  и , то есть определяет рассеяние в любом направлении .

Приведем также выражение для амплитуды рассеяния в декартовых координатах

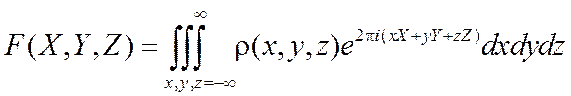                   .        (1.9)

Формулы (1.8) и (1.9) позволяют решать задачи о рассеянии от объектов различной формы, с различным расположением рассеивающих центров.

Пространство вектора , в котором задана функция , называется обратным пространством. Говорят, что  является «образом» в обратном пространстве функции , описывающей строение объекта в реальном пространстве.

Если объект определенным образом ориентирован по отношению к направлению , то в дифракционной картине реализуются лишь некоторые значения амплитуды, так как концы вектора  (1.4) могут располагаться лишь на сфере, описываемой вектором . Эта сфера называется сферой отражения или сферой Эвальда (рис. 1.2). На рис. 1.2 показано распределение интенсивности  на рентгенограмме, соответствующее сечению 1 обратного пространства, причем интенсивности, наблюдаемые при рассеянии в направлении , то есть под углом , пропорциональны квадрату модуля  соответствующего значения . Угол  определяется по соотношению (1.6).

Рис. 1.2. Схема дифракции, показывающая сферу Эвальда (1)

и сферу ограничения (2) в обратном пространстве

При изменении направления начального пучка , или, что то же самое, при изменении ориентации объекта относительно первичного пучка, получаются другие сечения обратного пространства (рис. 1.2) Таким образом можно найти значение  внутри «сферы ограничения», имеющей радиус 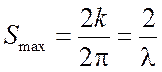. Отсюда следует, что величина используемой длины волны , вообще говоря, определяет объем информации, получаемой из экспериментальных данных. Поэтому длину волны нужно подбирать так, чтобы область, где 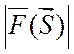 отлична от нуля, оказалась внутри сферы ограничения. В противном случае возникает «эффект обрыва».

Используем выражение (1.8) для изолированного сферически симметричного атома. Тогда для атомной амплитуды имеем выражение

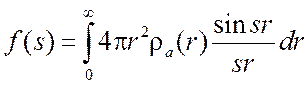                                   ,                           (1.10)

где  – электронная плотность атома, которая является функцией расстояния  от ядра. Атомная амплитуда в этом случае зависит только от величины модуля s (или ) и является в обратном пространстве сферически симметричной. Кривые атомного рассеяния, то есть зависимости , рассчитаны для всех атомов и для некоторых элементов представлены на рис. 1.3. Видно, что с увеличением угла происходит уменьшение f.

Найдем атомную амплитуду при . Так как 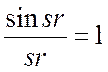 при , то