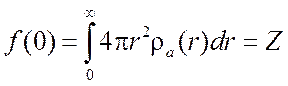,
(1.11)
где Z – число электронов в атоме. Поэтому рассеяние рентгеновских лучей тем сильнее, чем больше атомный номер элемента. Соответственно для водорода оно наименьшее.
|
|
Рис. 1.3. Амплитуды атомного рассеяния рентгеновских лучей.
Над кривыми указаны символы элементов
Рассмотрим
рассеяние группой атомов, центры которых расположены в точках 
. Распределение электронной плотности
в этом случае описывается суммой
.
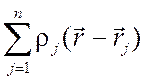(1.12)
Подставляя
(1.12) в соотношение (1.8) и учитывая, что для каждого из атомов применение (1.8)
даст атомную амплитуду (атомный или структурный фактор) 
,
находим амплитуду рассеяния от n атомов
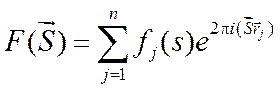. (1.13)
Эта
формула подобна формуле (1.7). Поэтому рассмотрение дифракции рентгеновских
лучей (а также электронов и нейтронов) группой атомов сводится к рассмотрению
дифракции на системе точек (центров атомов) с учетом зависимости от угла
атомной амплитуды. Спадание атомного фактора при увеличении S приводит к спаду амплитуды F
с увеличением S. Поэтому функция 
в обратном пространстве постепенно
уменьшается и не равна нулю только в пределах некоторых конечных значений S.
2. Физические принципы
рентгеноструктурного анализа глобулярных белков
Для рентгенографического изучения белок необходимо выделить из организма, где он находится в растворе и в смеси с другими белками. Далее после выделения нужно получить гомогенный препарат, в котором бы присутствовал один вид белковых молекул. Как оказалось, такие очищенные белки кристаллизуются, и это было очень важным открытием 20-30-х годов XX века. Особенностью белковых кристаллов является то, что они содержат воду и поэтому должны исследоваться в соответствующем растворе. Известно, что наиболее полную информацию о структуре вещества на основе рентгеноструктурного анализа можно получить, изучая кристаллы. Эти объекты дают очень богатую рефлексами дифракционную картину. Разработаны методы обработки рентгенографических данных, полученных от кристаллов белков. В данном разделе мы остановимся на методе рентгеноструктурного анализа кристаллов.
Для дальнейшего рассмотрения необходимо использовать некоторые элементы кристаллографии, которые приводятся ниже.
Под пространственной решеткой понимают такое расположение точек («узлов» решетки), при котором каждая точка находится в таком же окружении и в такой же ориентации, что и любая другая. Отметим, что эта решетка из точек дает лишь конкретное изображение того, каким образом мотив, составленный из группы атомов, повторяется в пространстве.
Структуру кристалла описывают с помощью элементарных ячеек, то есть некоторого основного параллелепипеда (рис. 2.1), многократным последовательным повторением которого можно получить структуру всего кристалла. Такая ячейка должна содержать полную информацию о той группировке атомов или молекул, повторением которой может быть построен кристалл. Обычно выбирают элементарную ячейку, которая имеет наиболее короткие ребра и симметрию, максимально возможную для данного кристалла. В связи с этим кристалл можно характеризовать числом z элементарных ячеек в единице объема кристалла
,
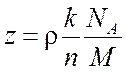где r – плотность
кристалла, k – число одинаковых атомов в
химической формуле соединения, 
– постоянная
Авогадро, n – число одинаковых атомов,
приходящихся на элементарную ячейку, М – молярная масса вещества. Ребра
ячейки задаются тремя векторами: 
, 
и 
,
а углы между ними обозначают буквами a,
b и g
(рис. 2.1). Длины ребер элементарной ячейки задаются модулями векторов а,
в и с. Положение любой точки в ячейке определяется координатами,
причем за оси принимают ребра ячейки, а за единицу длины вдоль каждой оси –
длину ребра.
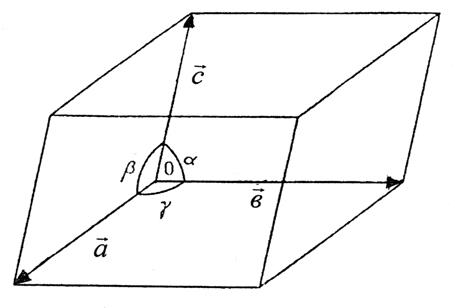
Рис. 2.1. Элементарная ячейка
При изучении кристаллических структур очень важным является
понятие о симметрии. В связи с этим вводится определение симметрически
независимой части ячейки, то есть основного повторяющегося мотива (или
объекта), который связан со всеми другими идентичными мотивами внутри
элементарной ячейки операциями симметрии, а с содержимым других элементарных
ячеек – трансляциями , и
.
Выделяют три основных типа операций симметрии: зеркальную плоскость, поворотную ось и инверсионную ось.
Зеркальная плоскость (ее обозначают буквой m) – это отражение в плоскости симметрии. Известно, что биологические объекты состоят из молекул, которые являются оптически активными (например, аминокислоты, входящие в состав белков), т.е. существующими в одной из двух возможных энантиоморфных форм. Поэтому данный тип операций, переводящий правую молекулу в левую и наоборот, не встречается в кристаллах биологических макромолекул.
Поворотная ось порядка х. В этом случае для получения идентичного положения поворот должен быть сделан на угол 3600/х. Например, оси 2-го порядка соответствует поворот на 1800, оси 3-го порядка – на 1200 и т.д. В кристаллах возможны только поворотные оси, порядок которых принимает следующие значения: 1, 2, 3, 4 и 6.
Инверсионная ось является комбинацией поворота порядка
х и отражения в точке, то есть поворот + инверсия. Она обозначается в
зависимости от поворота 
, 
, 
, 
и 
.
Например, ось эквивалентна центру
симметрии, ось – зеркальной плоскости.
Указанные элементы симметрии можно скомбинировать различным образом. Если несколько элементов симметрии имеют одну общую точку, то они образуют так называемую точечную группу. Применение всех операций симметрии точечной группы к любой точке структуры возвращает ее в исходное положение. Можно отметить, что число возможных комбинаций ограничено. Например, две поворотные оси 2-го порядка нельзя соединить под любым углом. Кроме этого, различные комбинации могут оказаться эквивалентными. Так, поворотная ось 2-го порядка и плоскость симметрии, проходящая через нее, образуют ту же группу, что и две взаимно-перпендикулярные плоскости симметрии, пересекающиеся по этой оси.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
