Основы теории рентгенографических исследований. Физические принципы рентгеноструктурного анализа глобулярных белков (Разделы 1-2 учебного пособия "Рентгенография биологических объектов"), страница 10

Кратко остановимся на получении тяжелоатомных производных. Как было отмечено ранее, введение тяжелого атома в определенное положение на поверхности белка может быть достигнуто за счет вытеснения растворителя без нарушения структуры как молекулы белка, так и кристалла. Однако, как отмечено в литературе, получение тяжелоатомных производных является процессом проб и ошибок. Получение таких производных требует детального знания кристаллической структуры белка. Некоторые указания по выбору подходящих тяжелых атомов дает знание аминокислотной последовательности белка. Однако часть аминокислот находится в центре молекулы белка или участвует в осуществлении контактов между молекулами в решетке и из-за этого является недоступной для присоединения тяжелого атома. Кроме того, некоторые присоединения обусловлены геометрией расположения белка в решетке и не являются специфическими. Все это затрудняет связывание тяжелого атома с молекулой белка. Тем не менее, накоплен большой опыт в этой области и определены наиболее удачные способы получения изоморфных производных. Например, если белок содержит кофактор, являющийся ионом металла (цинк, кальций), то тяжелоатомное производное может быть получено путем замещения такого кофактора тяжелым атомом. Другими способами получения тяжелоатомных производных может быть использование специфических ингибиторов ферментов и транспортных белков, меченых тяжелыми атомами, а также аналогов аминокислотных остатков, имеющих тяжелоатомную метку.

Тяжелоатомные производные можно приготовить несколькими различными методами. Наиболее успешным оказался метод, в котором осуществляется выдерживание кристаллов белка в растворе, содержащем тяжелые атомы. Эти атомы диффундируют по каналам, имеющимся в кристаллах, и тем самым получают доступ к молекулам белка в кристаллической решетке. Другой метод состоит в добавлении тяжелых атомов в кристаллизационную среду. В результате этого осуществляется совместная кристаллизация и в молекулы белков включаются тяжелые атомы. Наконец, есть химический способ получения тяжелоатомных производных, заключающийся в том, что перед кристаллизацией проводится реакция, в результате которой образуются ковалентные связи тяжелого атома с некоторыми группами белка. Последние два способа имеют недостатки, заключающиеся в том, что тяжелый атом изменяет взаимодействие между белками в растворе, что мешает кристаллизации или приводит к образованию кристаллов, которые не являются изоморфными кристаллам нативного белка.

Если в структуре есть аномальные рассеиватели, то обнаруживаются нарушения закона Фриделя, и это также можно использовать для решения фазовой проблемы.

В случае аномального рассеяния рассеивающая способность (фактор рассеяния) f является комплексной величиной и включает в себя действительную  и мнимую  части:

.          (2.25)

Для большинства атомов, входящих в состав белков (углерод, азот, кислород, водород), коэффициенты поглощения на излучении  очень малы. Поэтому в кристаллических структурах белков можно игнорировать мнимую часть фактора рассеяния и учитывать только действительную составляющую.

Рассмотрим структурные амплитуды прямого и инвертированного отражений для нативного белка:

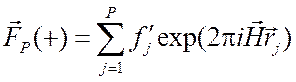 для hkl,          (2.26)

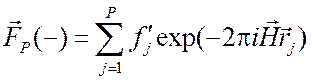 для ,          (2.27)

где черточки означают отрицательные значения индексов hkl. Суммирование производится по всем атомам элементарной ячейки. В этом случае абсолютные величины структурных амплитуд для отражений hkl и  равны (закон Фриделя).

Теперь рассмотрим изоморфное производное, т.е. кристаллическую структуру белка, к которому присоединены какие-нибудь тяжелые атомы, например атомы урана. В этом случае фактор рассеяния уже нельзя считать чисто вещественным, поэтому он будет определяться следующим выражением:

.          (2.28)

Тогда вклад тяжелого атома в прямое отражение кристалла производного может быть выражен как

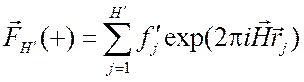          (2.29)

и

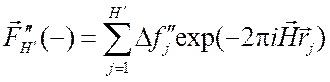          (2.30)

для действительной и мнимой частей соответственно, причем  – число тяжелых атомов в элементарной ячейке. Соответствующие выражения можно написать и для инвертированного отражения. Тогда для прямого и инвертированного отражений тяжелоатомного производного можно записать:

,          (2.31)

.           (2.32)

Если представить эти соотношения в виде векторных диаграмм (рис. 2.12), то можно видеть, что в общем случае , т.е. закон Фриделя уже не выполняется.

Рис. 2.12. Векторные диаграммы структурных факторов прямого

 и инвертированного отражений. Р – атомы, рассеивающие нормально,

Н – атомы, рассеивающие аномально

Разности аномального рассеяния, т.е. величины , наблюдаются только когда аномальные рассеиватели находятся среди неаномальных рассеивателей. Если же кристалл состоит целиком из одних аномальных рассеивателей, то он подчиняется закону Фриделя.

Следует также отметить, что в большинстве случаев разности аномального рассеяния имеют малую величину и на рентгенограммах их бывает сложно заметить визуально. Поэтому очень важно при их выявлении производить измерения с большой точностью. Такие пары должны быть измерены почти одновременно, чтобы радиационное повреждение образца, движение жидкости в капилляре с образцом или изменение напряжения на рентгеновском генераторе не отразились на разностях.

Далее рассмотрим, как используются разности аномального рассеяния для определения фаз. Связь аномальных разностей  можно найти из рис. 2.13. Используя теорему косинусов, из этого рисунка находят разность аномального рассеяния:

,

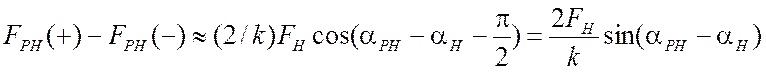где .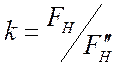

Поэтому фаза  тяжелоатомного производного определяется следующим выражением:

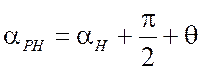,           (2.33)

где

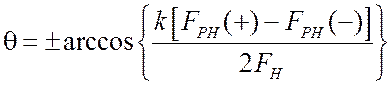.                                                                                                           (2.34)