Основы теории рентгенографических исследований. Физические принципы рентгеноструктурного анализа глобулярных белков (Разделы 1-2 учебного пособия "Рентгенография биологических объектов"), страница 5

Четырнадцать решеток Браве не исчерпывают всех возможных способов построения кристалла с заданной макроскопической структурой. Для полного описания структуры кристаллов добавляют еще две трансляционные операции: плоскость скольжения и винтовые оси. Плоскость скольжения соответствует операции отражения в плоскости и переноса параллельно этой плоскости на расстояние, равное половине длины ребра элементарной ячейки. В кристаллах белков такие плоскости отсутствуют. Винтовой оси соответствуют поворот на угол, равный порядку оси, и перенос параллельно оси поворота. Так, для винтовой оси 2-го порядка перенос составляет половину длины ребра элементарной ячейки, параллельного оси вращения. Винтовая ось 2-го порядка обозначается 2₁.

В случае винтовой оси 3-го порядка перенос может быть на одну треть (3₁) или на две трети (3₂) ребра элементарной ячейки. Для винтовой оси 4-го порядка есть три варианта переноса соответственно на одну четверть (4₁), две четверти (4₂) и три четверти (4₃) ребра элементарной ячейки. Винтовые оси 6-го порядка обозначаются 6₁, 6₂, 6₃, 6₄, 6₅ и соответствуют переносу на одну шестую, две шестых, три шестых, четыре шестых и пять шестых ребра элементарной ячейки.

Таким образом, полный набор комбинаций элементов симметрии для описания кристаллической структуры должен учитывать элементы внешней симметрии, которые представляются 32 видами, элементы внутренней симметрии, которые характеризуются четырнадцатью решетками Браве и трансляционными операциями симметрии. Такие комбинации из элементов симметрии называются пространственными группами. Их общее число равно 230. При обозначении этих групп приняты следующие правила. Тип решетки Браве указывается прописной буквой: Р – примитивная ячейка, F – гранецентрированная, I – объемноцентрированная. А, В и С означают соответственно, что в ячейке центрирована только одна грань. Затем следует символ точечной группы, из которой выводится пространственная, причем в этом символе некоторые поворотные оси заменяют винтовыми, а некоторые зеркальные плоскости – плоскостями скольжения.

В силу того, что биологические молекулы, как было отмечено ранее, являются оптически активными, число пространственных групп, которыми описываются кристаллы белков, уменьшается и составляет 65. Это так называемые энантиоморфные пространственные группы, которые представлены в табл. 2.2.

Таблица 2.2

Энантиоморфные пространственные группы

Сингония	Символы пространственных групп
Триклинная	Р1
Моноклинная	Р2, Р21, С2
Ромбическая	С222, Р222, Р212121, Р21212, Р2221, С2221, F222, I222, I212121
Тетрагональная	Р4, Р41, Р42, Р43, I4, I41, Р422, Р4212, Р4122, Р41212, Р41212, Р422, Р42212, Р43212, Р4322, I422, I4122
Тригональная	Р3, Р31, Р32, R3, Р312, Р321, Р3121, Р3112, Р3212, Р3221, R32
Гексагональная	Р6, Р65, Р64, Р63, Р62, Р61, Р622, Р6122, Р6222, Р6322, Р6422, Р6522
Кубическая	Р23, F23, I23, Р213, I213, Р432, Р4132, Р4232, Р4332, F432, F4132, I432, I4132

Более полные сведения о 230 пространственных группах можно получить из Международных таблиц, т. 1. В случае кристаллов из биологических молекул наиболее часто встречаются следующие три пространственные группы: моноклинная группа Р2₁, ромбическая группа Р2₁2₁2₁ и тетрагональная группа Р4₁2₁2.

Кратко рассмотрим расположение элементов симметрии в моноклинной группе Р2₁, которая основана на точечной группе 2. Решетка, как следует из обозначения, является в этом случае примитивной, а винтовая ось проходит параллельно оси  элементарной ячейки через ее начало. На рис. 2.3 показаны проекции структуры вдоль двойной винтовой оси  (верхняя часть) и вдоль оси  (нижняя часть), где винтовые оси обозначены стрелками. Точка с координатами x, y, z элементарной ячейки переводится действием элемента симметрии в положение . В результате порождается набор двойных винтовых осей, которые расположены в серединах ребер  и  и показаны на рисунке. Элементарная ячейка в этом случае содержит две молекулы. Сама структура не является центросимметричной, но ее проекция на плоскость xz центросимметрична относительно начала.

Рис. 2.3. Пространственная группа Р2₁ (из Международных таблиц

по рентгеновской кристаллографии, т. 1)

Формула (1.13) позволяет рассчитать амплитуду рассеяния не только от молекул (или их групп), но и от кристаллов. В кристалле атомы или группировки атомов расположены периодически в трех измерениях. Поэтому электронная плотность  кристалла является периодической функцией координат . Для одномерного кристалла интеграл Фурье типа (1.9) записывается следующим образом:

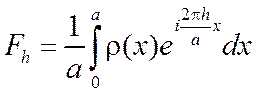                                  ,                                    (2.1)

где а – период кристаллической решетки, а  – периодическая функция электронной плотности. В данном случае имеется не непрерывный набор амплитуд , а дискретные значения коэффициентов Фурье  [h – целые числа; для нецелочисленных h интеграл (2.1) равен нулю]. Сравнивая (1.8) и (2.1), можно заключить, что величины  отличны от нуля только при значениях :

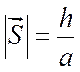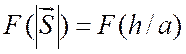                                            ,                                  (2.2)

а расстояния между ними равны .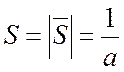

Формулу (2.1) можно обобщить на трехмерный случай:

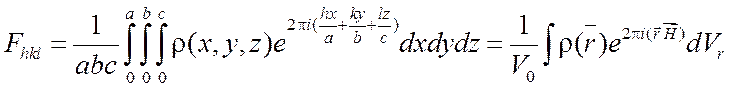.    (2.3)

Здесь  – периоды кристаллической решетки;  – объем ячейки;  – целые числа. В формуле (2.3) введен вектор , компонентами которого в обратном пространстве являются 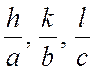. Поэтому при дифракции на кристалле амплитуда рассеяния отлична от нуля только при указанных величинах компонент вектора , а распределение таких точек будет периодично в обратном пространстве и представляет собой обратную решетку (рис. 2.4), каждая точка которой (узел ) определяет вектор обратной решетки