Начертательная геометрия: Учебное пособие

Министерство образования Российской Федерации

Рязанская государственная радиотехническая академия

В.П. СТРЕЛЬНИКОВ

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Учебное пособие

Рязань 2004

УДК 515(015)

          Начертательная геометрия: Учеб. пособие   / В.П. Стрельников;

Рязан. гос. радиотехн. акад. Рязань, 2004. 52 с.

          Содержит краткие сведения по основным разделам теории начертательной геометрии. Каждый раздел сопровождается иллюстрированными примерами чертежей и показывается методика их построения. Для каждого раздела приведены варианты заданий для студентов.

          Предназначено для студентов дневной и заочной формы обучения.

          Табл. 1. Ил. 116. Библиогр.: 6 назв.

           Начертательная геометрия, точка, линия, плоскость, поверхность.

            Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.

             Рецензент: кафедра начертательной геометрии и черчения Рязанской государственной радиотехнической академии.

С т р е л ь н и к о в   Виктор Павлович

Начертательная геометрия

Редактор Р.К. Мангутова

Корректор Н.А. Орлова

Лицензия № 020446.

             Подписано в печать 20.10.04. Формат бумаги 60x84 1/16.

               Бумага газетная. Печать трафаретная. Усл. печ. л. 3,25.

Уч.-изд. л. 3,25. Тираж 100 экз. Заказ

                Рязанская государственная радиотехническая академия.

390005, Рязань, ул.Гагарина, 59/1.

Редакционно-издательский центр РГРТА.

                                                        ©  Рязанская государственная

                                                                радиотехническая академия, 2004

Введение

Начертательная геометрия является тем разделом геометрии, в котором изучают способы изображения пространственных форм (линий, плоскостей, поверхностей) на плоскости чертежа и решают позиционные и метрические задачи по заданным изображениям данных форм.

К позиционным задачам относятся задачи, в которых выясняются позиционные отношения между геометрическими элементам. Это задачи на их видимую принадлежность или пересечение.

К метрическим относятся задачи, в которых определяются измеряемые величины: это расстояния между геометрическими элементами и углы между ними.

Любое инженерное творчество – это создание каких-то геометрических образов. Способами начертательной геометрии и графическими построениями осуществляется конструирование этих образов. Инженер получает информацию зрением, а не обонянием или слухом. Составлением и обработкой этой информации занимается начертательная геометрия. Обмен информацией между людьми осуществляется в виде закодированной геометрии. Роль начертательной геометрии возрастает в связи с компьютеризацией процессов конструирования. Способы начертательной геометрии – это единственные способы при конструировании поверхностей.

Начертательная геометрия – единственная наука, формирующая пространственное мышление. Она является основой инженерного образования.

Система обозначений геометрических образов и действий

А, B, C … – точки пространства (заглавные буквы латинского алфавита)

a, b, c … – линии в пространстве (строчные буквы латинского алфавита)

α, β, γ … – плоскости, поверхности (строчные буквы греческого алфавита)

[AB] – отрезок прямой

A^α – проекция точки А на плоскость α

|| – параллельность

 – пересечение, например [AB]  [CD] = K

 – взаимная принадлежность, например a  α (линия a принадлежит плоскости или поверхности α)

≡ – совпадение геометрических образов

Метод проекций

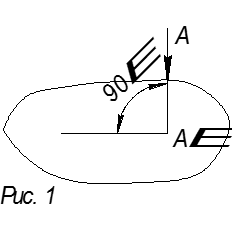
Через точку А проведём прямую S перпендикулярно к плоскости α (рис. 1). Прямая S есть направляющая или проецирующая прямая.

Плоскость α – плоскость проекции. Точка A^α есть проекция точки А, которая получается от пересечения прямой S с плоскостью α. Такое проецирование называется прямоугольным или ортогональным .

В случае, когда угол между S и α не равен 90°, проецирование называется косоугольным.

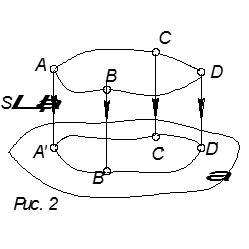
На рис. 2 проекция фигуры Ј (Ј^α) есть множество проекций её точек. Проецирующие прямые S параллельны друг другу.

Такое проецирование называется параллельным.

Инвариантные (неизменные) свойства параллельного проецирования

1.  Проекция точки есть точка.

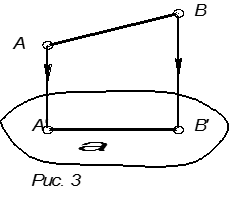
2.  Проекция прямой есть прямая, если она не совпадает с направлением проецирования (рис. 3). Для любой прямой, параллельной S (совпадающей с направлением проецирования), проекция прямой является точка (рис. 4).

Рис.4

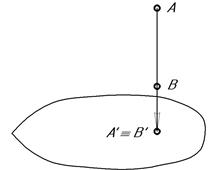
3. а) если точка принадлежит линии, то проекция точки принадлежит проекции линии;

     б) если линия принадлежит поверхности или плоскости, то проекция линии принадлежит  проекции поверхности или плоскости;

     в) если точка принадлежит линии и линия принадлежит плоскости или поверхности, то проекция точки принадлежит проекции поверхности или плоскости;

     г) если фигура принадлежит поверхности или плоскости и поверхность или плоскость параллельна направлению проецирования, то проекция этой фигуры принадлежит их следу (рис. 5).

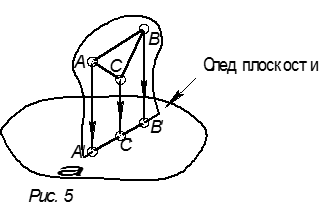
4.  Если прямые в пространстве параллельны, то проекции этих прямых также параллельны.

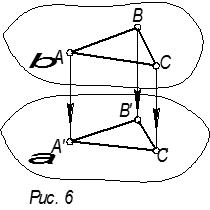
5.  Если фигура принадлежит поверхности и поверхность параллельна плоскости проекции, то проекция этой фигуры равна самой фигуре (рис. 6).

6.  При ортогональном (прямоугольном) проецировании, если одна сторона прямого угла параллельна плоскости проекции и другая сторона не перпендикулярна к плоскости проекции, то проекция прямого угла есть прямой угол (рис. 7).

пл.  α || пл. β

∆ABC = ∆A′B′C′

AB || α BC не  α

ABC = 90° A′B′C′ = 90°

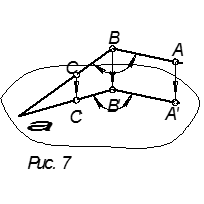
Прямоугольное (ортогональное) проецирование точки на три плоскости проекции

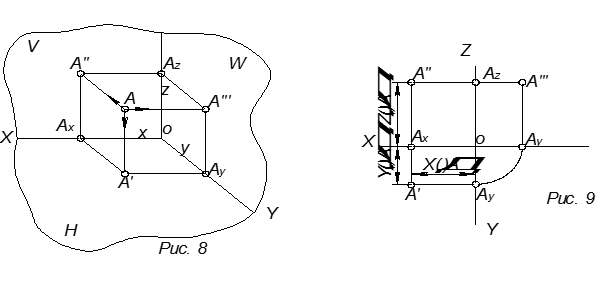
Положение точки (а следовательно, и любой геометрической фигуры) может быть определено, если будет задана какая-нибудь координатная система. Очень удобной для фиксации геометрической фигуры является декартова система координат (Декарт – французский математик и философ), состоящая из трёх взаимно-перпендикулярных плоскостей проекций. В пространстве трёхгранного угла, образованного плоскостями проекций: V (вертикальной), H (горизонтальной), W (профильной), точка определяется тремя координатами: X, Y и Z. Линии пересечения плоскостей проекций образуют оси координат X, Y и Z. Точка пересечения координатных осей (точка О) принимается за начало отсчёта координат.

Пользоваться пространственным макетом (рис. 8) для отображения ортогональных проекций неудобно из-за его громоздкости. Поэтому пользуются эпюром, т.е. чертежом, составленным из двух или более связанных между собой проекций геометрических фигур (рис. 9).

Преобразование пространственного макета в эпюр производится совмещением плоскостей H и W с фронтальной плоскостью проекции V.

На рис. 9 изображены три проекции точки A, причём проекция точки A′′′ может быть построена следующим образом.