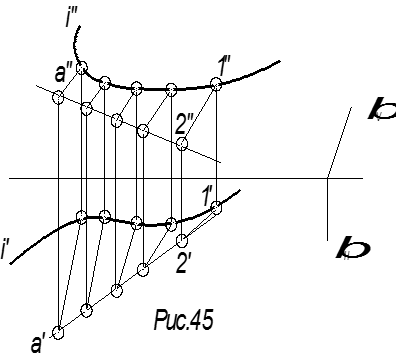
Образован направляющими l1 и l2 – это гладкие кривые линии. Образующие (например, 1-2) параллельны некоторой заданной плоскости параллелизма a (1¢-2¢ || aH) (рис. 45).
|
Коноид
|
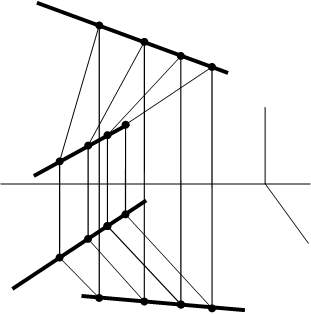
Гиперболический
параболоид
(косая плоскость)
![]()
![]()
![]()
![]()
![]()
![]() Образован
скольжением образующей (например, 1-2) по двум скрещивающимся прямолинейным
направляющим m и n. При этом образующая в каждом своем положении остается
параллельной плоскости параллелизма a
(1¢-2¢ || aН), (рис. 47а).
Образован
скольжением образующей (например, 1-2) по двум скрещивающимся прямолинейным
направляющим m и n. При этом образующая в каждом своем положении остается
параллельной плоскости параллелизма a
(1¢-2¢ || aН), (рис. 47а).
|
![]()
![]()
|
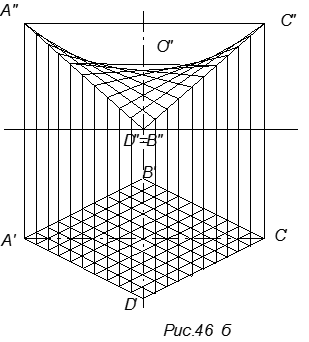
В данном примере (рис. 47б) косой плоскости направляющих плоскостей параллелизма две: первой плоскости параллелизма параллельны образующие одной системы – это AD и BC, второй - образующие другой системы – это AB и CD. Плоскости параллелизма на рисунке не указаны.
Нелинейчатые поверхности с образующей переменного вида
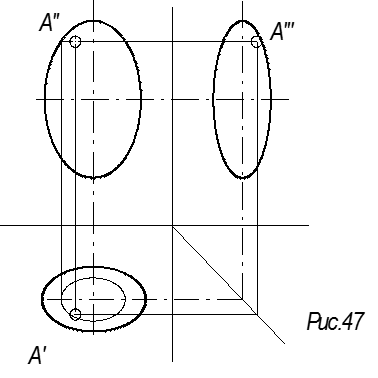
Трехосный эллипсоид
Образуется двумя направляющими эллипсами и деформирующейся образующей, тоже эллипсом, который начинается с одной точки, максимально расширяется в середине поверхности и снова превращается в точку, скользя по двум направляющим эллипсам (рис. 48).
Эллиптический параболоид
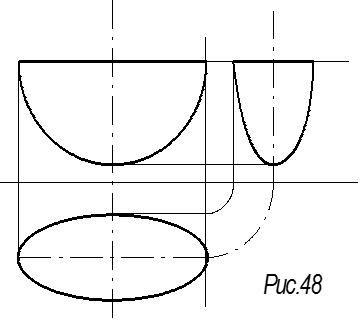
 Образуется
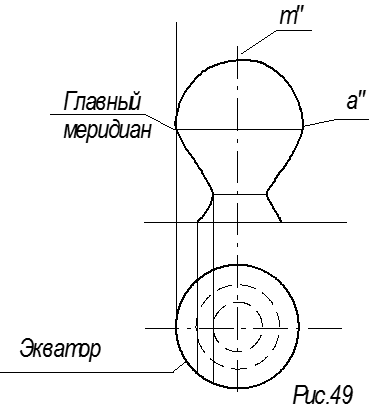
двумя направляющими параболами и деформирующимся эллипсом (рис. 49).
Образуется
двумя направляющими параболами и деформирующимся эллипсом (рис. 49).
Поверхность вращения общего вида
Это поверхность, образованная произвольной кривой (плоской или пространственной), при этом она вращается вокруг неподвижной оси.
В определители поверхности входят образующая a, ось вращения m.
![]()
|
 Каждая точка образующей а
при вращении вокруг оси описывает окружность. Эти окружности называют параллелями.
Наибольшая параллель называется экватором, наименьшая – горлом (шейкой)
Каждая точка образующей а
при вращении вокруг оси описывает окружность. Эти окружности называют параллелями.
Наибольшая параллель называется экватором, наименьшая – горлом (шейкой) 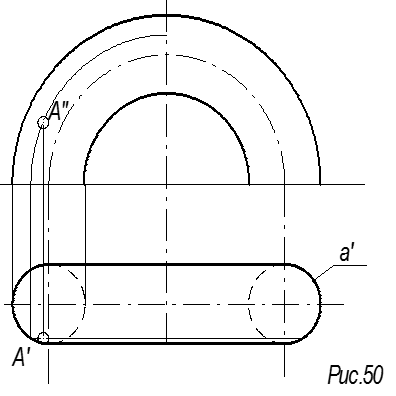
Поверхности вращения частного вида
Тор – поверхность, образованная вращением окружности а (образующая) вокруг оси i (рис. 51).
|
Эллипсоид вращения
|
![]()
![]()
|
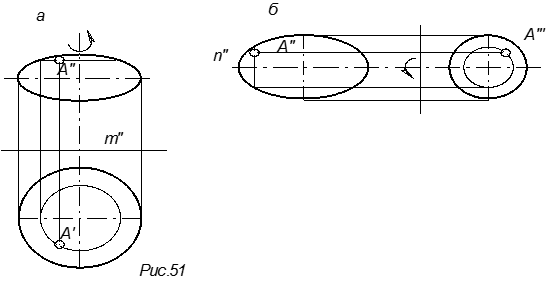
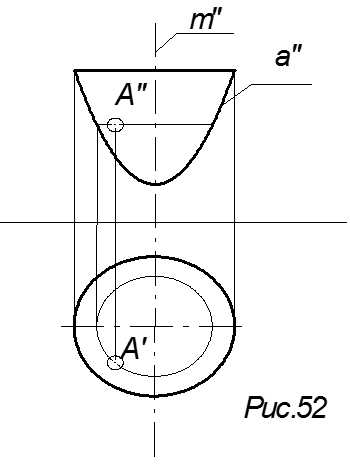
получим сжатый эллипсоид вращения (рис. 52 а).
Если вращение осуществлять вокруг большой оси n,
образуется поверхность вытянутого эллипсоида
вращения (рис. 52б).
Параболоид вращения
Образован вращением параболы а вокруг оси m (рис. 53).
|
Однополостный гиперболоид вращения
 Он в данном примере
(рис.54) образован прямолинейной образующей а путем вращения ее вокруг
оси l, скрещивающейся с ней. Плоскость,
перпендикулярная к оси однополостного гиперболоида, рассекает его в данном
случае по окружности.
Он в данном примере
(рис.54) образован прямолинейной образующей а путем вращения ее вокруг
оси l, скрещивающейся с ней. Плоскость,
перпендикулярная к оси однополостного гиперболоида, рассекает его в данном
случае по окружности.
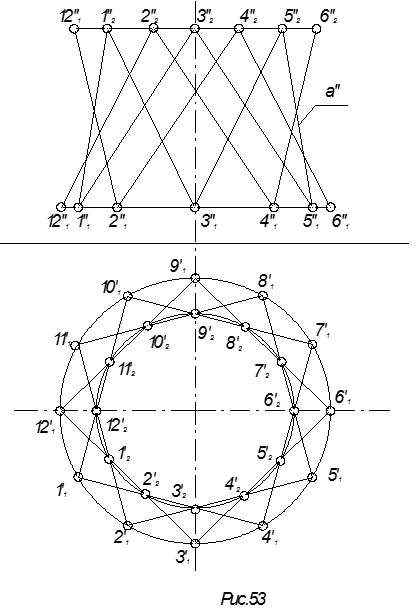
 Для построения проекций необходимо: разделить проекции окружностей на
произвольное равное число частей, затем соединить прямой линией точку 1² нижней окружности с любой (кроме 12²) точкой верхней окружности (это образующая).
На чертеже точка 11²
соединена с точкой 32²,
точка 21² с 42² и т.д. Соединив все точки деления нижней
окружности с точками деления верхней окружности, получим проекции каркаса
поверхности. Второй каркас этой же поверхности образован соединением первой
точки верхней окружности с третьей точкой нижней окружности, точка 22² - с точкой 41², 32² с 51² и т.д.
Для построения проекций необходимо: разделить проекции окружностей на
произвольное равное число частей, затем соединить прямой линией точку 1² нижней окружности с любой (кроме 12²) точкой верхней окружности (это образующая).
На чертеже точка 11²
соединена с точкой 32²,
точка 21² с 42² и т.д. Соединив все точки деления нижней
окружности с точками деления верхней окружности, получим проекции каркаса
поверхности. Второй каркас этой же поверхности образован соединением первой
точки верхней окружности с третьей точкой нижней окружности, точка 22² - с точкой 41², 32² с 51² и т.д.
Плоскость, проходящая через ось (i) поверхности, пересекает построенную поверхность по гиперболе. Отсюда и произошло название этой поверхности.
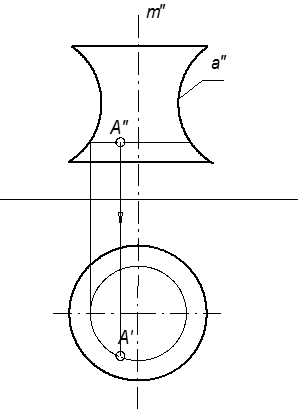
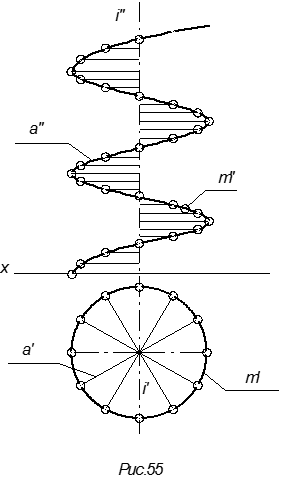
Поверхность однополостного гиперболоида вращения можно получить также вращением гиперболы (а) вокруг ее мнимой оси (m), (рис. 55а)
|
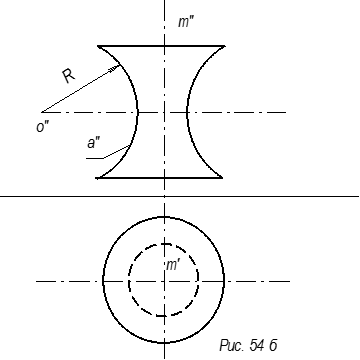
Образующей а поверхности вращения, называемой глобоидом, является дуга окружности радиусом R (рис. 55б), а ось вращения линия m (m”-m’)
|
Винтовые поверхности
Поверхность называется винтовой, если она получается винтовым перемещением образующей линии. Данное перемещение характеризуется вращением этой линии вокруг оси и одновременно поступательным движением, параллельным этой оси.
Линейчатые винтовые поверхности называются геликоидами. Если образующая имеет угол с осью равный 90°, то геликоид называют прямым (рис.56), если угол произвольный, отличный от 0° и 90°, то геликоид называют косым или наклонным (рис.57).
|
|
|
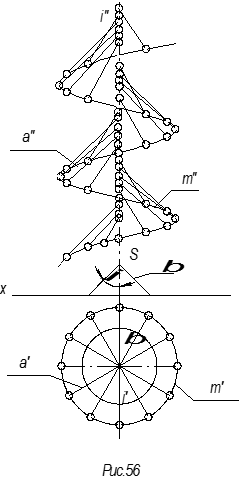
Линия а – образующая Винтовая линия m – направляющая
Винтовая линия m – направляющая Линия а – образующая, параллельная
образующей конуса b
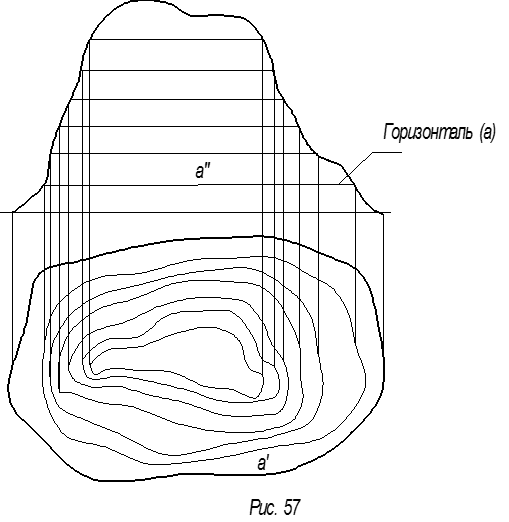
Поверхности, задаваемые каркасом
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.