Начертательная геометрия: Учебное пособие, страница 6

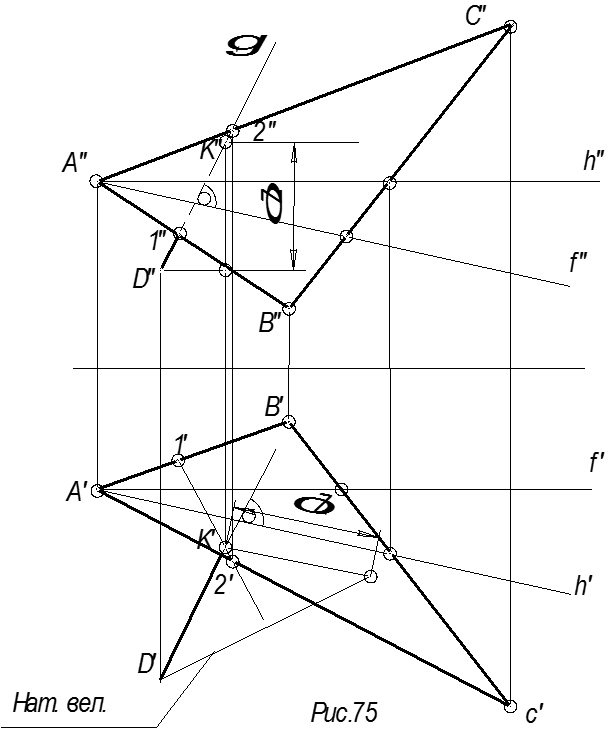
В соответствии с признаком перпендикулярности прямой и плоскости в плоскости DАВС (рис.76) проводим две пересекающиеся прямые – горизонталь h и фронталь f, являющиеся наиболее выгодными прямыми, могущими составлять угол 90° с прямой, проведенной через т. D  непосредственно на чертеже, в соответствии с инвариантным свойством проецирования прямого угла. При этом фронтальная проекция перпендикуляра составляет угол 90° с фронтальной проекцией фронтали f (D²K² ^ f²), а горизонтальная проекция перпендикуляра составляет угол 90° с горизонтальной проекцией горизонтали h (D¢K¢ ^ h¢). Надо сказать, что искомый перпендикуляр с горизонталью и фронталью скрещивается под углом 90°. В дальнейшем находим точку встречи перпендикуляра с плоскостью треугольника DАВС (точка К¢). Натуральную величину его находим способом прямоугольного треугольника.

Рис.76

 

Определение углов  ^Ùj° = ?

Пример 1

Определить величину угла между двумя плоскостями ∆АВС и ∆BCD.

x₁ || B¢C¢ ® пл. V₁ || BC

x₂ ^ B²₁C²₁ ® пл. H₁ ^ BC

 

Ða°  истинный

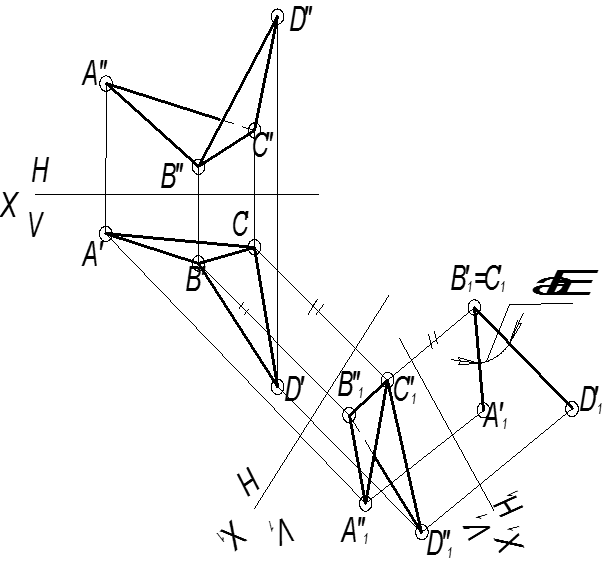                                                                           (рис. 77)

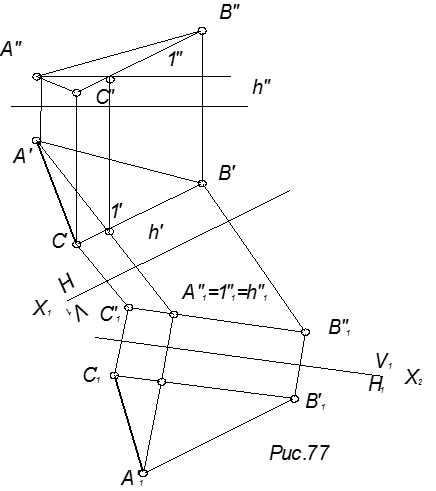
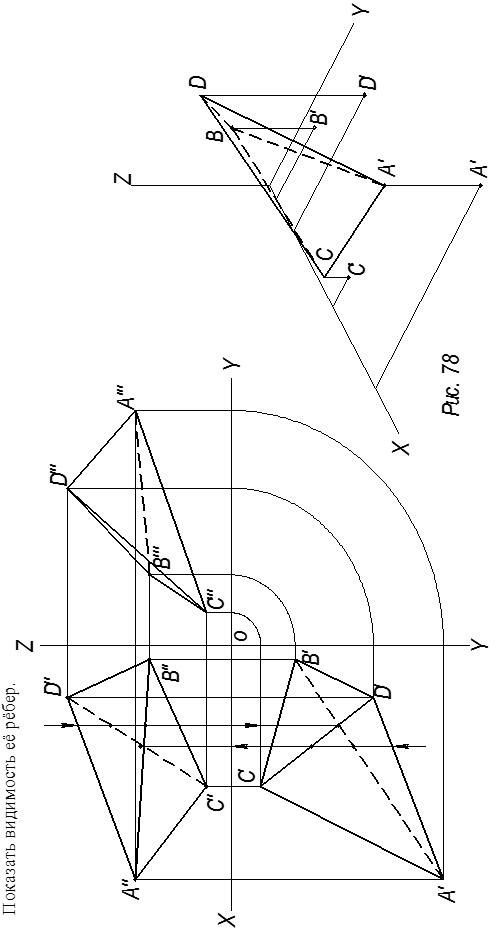
Пример 2

Определить натуральную величину DАВС.

x₁ ^ горизонтали h (h¢)

                                                                      пл. V₁ ^ горизонтали h

x₂ || A²B²C²

                                                                      пл. DABC || пл. H₁

 

                                                                      D A¢₁B¢₁C¢₁ - нат. величина

(рис.78)

 

 

№ вар	A			B			C			D
	X	Y	Z	X	Y	Z	X	Y	Z	X	Y	Z
1	16	14	90	86	80	26	132	52	82	75	85	110
2	20	10	92	85	80	25	136	50	84	68	85	112
3	16	12	86	80	72	20	132	48	82	70	82	106
4	21	9	39	84	80	109	136	49	48	70	84	19
5	118	8	86	52	78	26	0	52	86	72	86	110
6	20	14	90	86	80	26	136	50	85	70	85	112
7	110	85	10	54	28	82	0	80	45	65	105	80
8	18	91	9	83	26	80	134	84	47	67	109	84
9	116	10	90	52	80	26	0	44	82	72	86	108
10	18	40	76	83	118	5	134	48	39	68	19	0
11	116	12	94	50	82	26	0	52	86	70	86	108
12	124	96	12	52	22	75	0	82	48	70	118	86
13	17	10	45	83	80	112	134	49	45	68	84	19
14	19	79	40	84	6	108	133	39	48	68	0	20
15	120	90	10	50	25	80	0	85	50	70	110	85
16	18	13	86	86	81	25	134	51	80	70	86	111
17	117	10	39	51	80	110	0	47	48	68	84	19
18	116	39	8	53	110	80	0	48	47	68	19	84
19	20	39	10	84	109	78	136	48	47	69	19	86
20	122	39	76	51	109	7	0	49	39	139	19	0
21	121	38	74	50	107	5	0	46	40	135	19	0
22	19	41	9	82	110	80	136	47	47	68	19	86
23	117	41	75	51	108	7	0	48	37	134	21	0
24	116	75	39	51	5	108	0	38	46	136	45	19
25	118	89	10	53	26	80	0	70	49	68	111	86
26	122	10	88	50	84	22	0	54	84	66	82	112
27	120	10	90	54	80	26	0	50	86	70	88	110
28	90	35	20	170	55	60	110	130	120	35	60	135