Начертательная геометрия: Учебное пособие, страница 2

Из фронтальной проекции точки (A′′′) проводим прямую, -ю оси Z, и на этой прямой от оси Z откладываем отрезок равный, координате Y точки. Следует заметить, что две проекции точки A′′ и A′  вполне определяют положение точки в пространстве, поэтому чаще всего на эпюре изображают две проекции геометрического образа (как правило, на горизонтальной и фронтальной плоскостях).

Пример. Построить точку A с координатами X=50, Y=40, Z=60 (рис.10).

Эпюр прямой линии

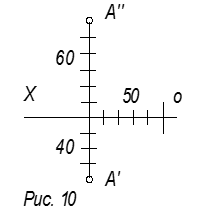
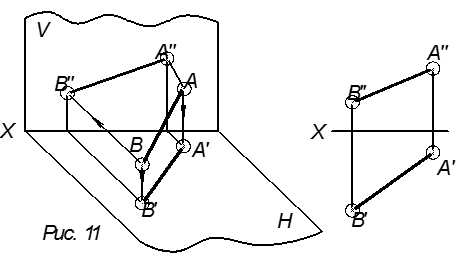
A(Y,Z) Y≠Z

B(Y,Z) Y≠Z

Это прямая общего положения.

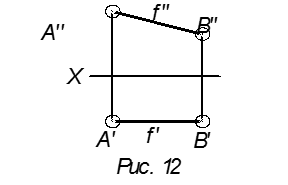
Y(·)A = Y(·)B, A′B′ || x

Z(·)A ≠ Z(·)B, AB || пл. V

Это фронтальная прямая (фронталь),

 обозначается буквой f.

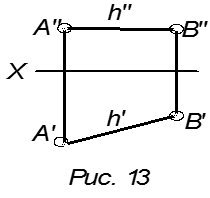                                      A′′B′′ || x

                                     A′B′ не || x

    AB || H

Это горизонтальная прямая (горизонталь).

Обозначается буквой h.

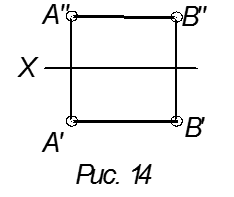
A′′B′′ || x      

   A′B′ || x             AB || H

                        Это линия уровня.

                        

 

   A′′ B′′  x         ABH

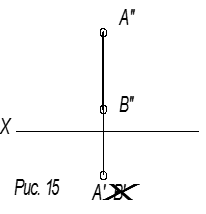
    A′ ≡ B′                AB || V

   Это горизонтально-проецирующая прямая.

   A′ B′  x        AB  V

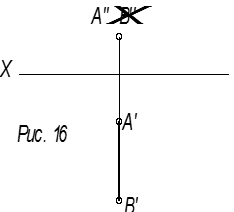
    A′′ ≡ B′′            AB || H

Это фронтально-проецирующая прямая.

Изображение плоскости

Плоскость может быть задана на чертеже:

1.  Тремя точками, не лежащими на одной прямой.

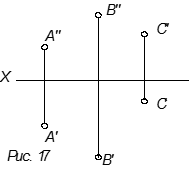
2.  Прямой и точкой вне прямой.

                                  

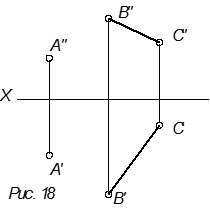
3.  Двумя пересекающимися прямыми линиями.

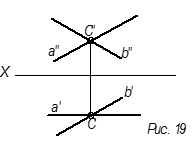
4.  Двумя параллельными прямыми линиями.

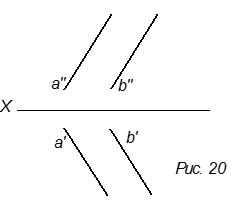
    О положении плоскости относительно плоскостей проекций удобно судить по её следам. Следами плоскости называются линии пересечения плоскости с плоскостями проекций.

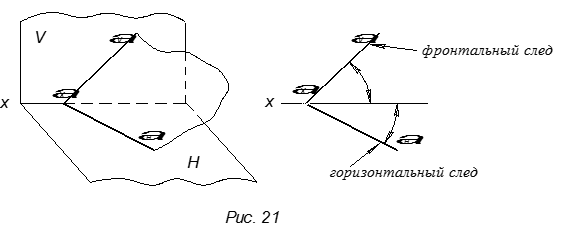На рис. 21 представлена плоскость общего положения.

Относительно плоскостей проекций плоскости могут занимать и частные положения.

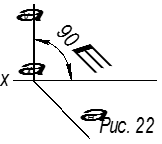
1.                                                                                                                                                                    α_V  x         пл. α  H

                Это горизонтально-проецирующая плоскость (рис.22).

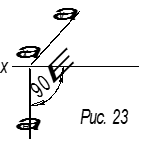2.                                        α_H x

                                      пл. α  V

             Это фронтально-проецирующая плоскость (рис.23).

3.

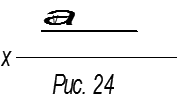          α_V || x

      пл. α || H

Это фронтально-проецирующая плоскость, называемая плоскостью уровня (рис.2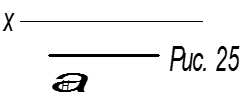4).    

4.  

                                             пл. α || V  α_H || x

         Это горизонтально-проецирующая плоскость, параллельная плоскости V (рис.25).

Аксонометрические (наглядные) проекции

В практике черчения часто бывает необходимо вместе с чертежом геометрической фигуры, выполненным в ортогональных проекциях, дать её наглядное изображение, состоящее только из одной проекции, т.е. путём параллельного проецирования предмета только на одну плоскость вместе с тремя осями координат (X, Y и Z).

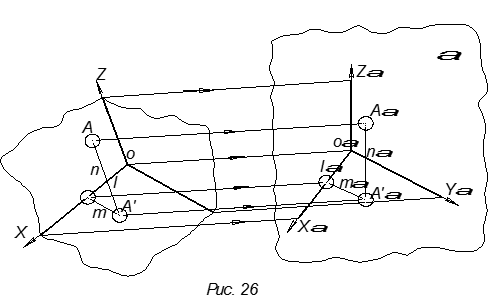
Пространственная координатная ломаная точка А(l + m + n) (рис. 26) проецируется на одну плоскость проекций α в плоскую координатную ломаную точку A_α(l_α + m_α + n_α).

Отношение проекций любой из пространственных координат точки

 A_α(l_α, m_α или n_α) к натуральным, пространственным координатам этой точки называется показателем (коэффициентом) искажения по аксонометрическим осям.

                             

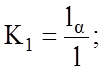
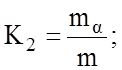
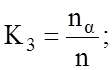
Если три коэффициента равны между собой, то аксонометрическая проекция называется изометрической.

Если равны между собой только два коэффициента, то проекция называется диметрической проекцией.

Если все коэффициенты не равны – проекция называется триметрической.

В начертательной геометрии рассматривается теорема о свойствах показателей искажения по аксонометрическим осям.

Вывод этой теоремы следующий:

Сумма квадратов показателей искажения по аксонометрическим осям равна двум:

В практике черчения чаще всего применяется изометрическая проекция, где все показатели равны между собой. И тогда получается .

, отсюда 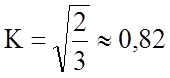:      X : Y : Z ≈ 0,82 : 0,82 : 0,82 

Это теоретическая изометрия.

Но показатель неудобен из-за своей двузначности, и его упрощают, приведя к единице. И тогда получается

X : Y : Z ≈ 1 : 1 : 1

Изометрия в последнем случае называется практической. Размеры с ортогональных проекций предметов без изменения переносятся в проекцию изометрическую.

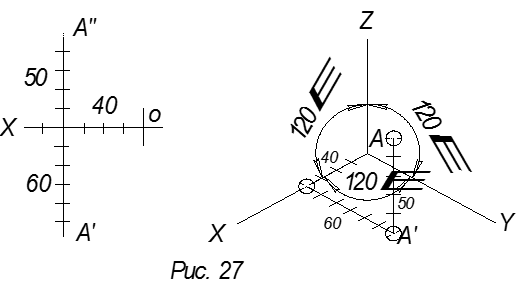
Пример. По заданным координатам точки А(40,60,50) построить три проекции в системе декартовых координат и прямоугольную изометрическую проекцию (рис.27).

Позиционные задачи

I.  Задачи на принадлежность

1.   Задать в плоскости произвольную прямую.

Признак принадлежности прямой и плоскости.

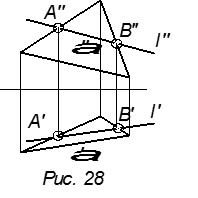Если две точки прямой принадлежат плоскости, то эта прямая принадлежит плоскости.

Чтобы задать в плоскости произвольную прямую, надо провести её через две точки, принадлежащие данной плоскости. Эти точки (рис. 28) A и B берём на сторонах плоскости треугольника.

 2.   Задать в плоскости произвольную точку.

                                                                            

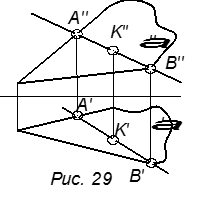
Эту точку  надо взять на прямой, принадлежащей плоскости (рис. 29).

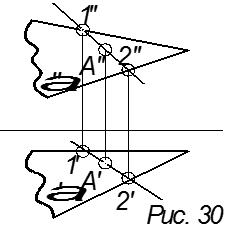 3. Зная одну проекцию точки, принадлежащей плоскости или поверхности, найти её вторую проекцию.

Для этого через заданную проекцию точки A на плоскости проводим произвольную прямую (1 – 2). Находим вторую проекцию проведённой прямой. Затем по линиям связи находим вторую проекцию точки

(рис. 30).

4.  Построить прямую принадлежащую проецирующей плоскости. На основании третьего инвариантного свойства (см. рис.5).

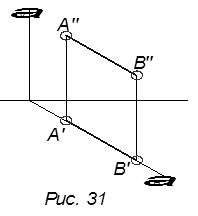Пл. α || направлению прямоугольного проецирования S (рис. 31).

5. 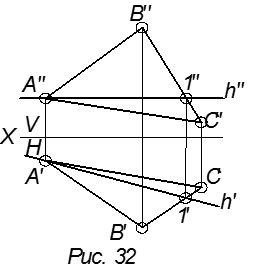 Построить горизонталь в плоскости.

Горизонталью в плоскости называется прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекции.

h′′ || X ,       горизонталь h || пл. H (рис. 32).

6.  Построить фронталь в плоскости.

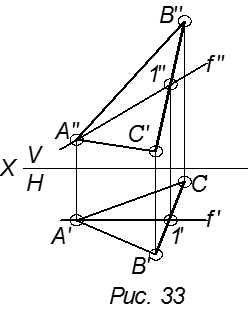
f′ || X,

фронталь f || пл. V (рис. 33).