Задачи на пересечение
1. Найти точку пересечения линии и поверхности в случае, когда поверхность проецирующая, а прямая не проецирующая.
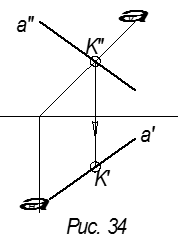
На основании третьего инвариантного свойства проекция точки K(K′′) принадлежит αV.
Проекцию K′ находим по линии связи (рис.34).
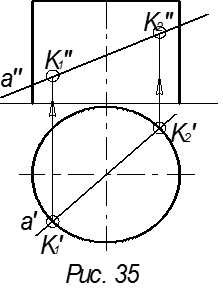
Так как искомые точки принадлежат проецирующей поверхности цилиндра (рис. 35), то на основании третьего инвариантного свойства горизонтальные проекции точек (K1′ и K2′) принадлежат горизонтальному следу цилиндра (окружность), а вертикальные проекции (K1′′ и K2′′) находят по линии связи (рис 35).
2. Найти точку пересечения линии и поверхности, когда прямая проецирующая, а поверхность не проецирующая.
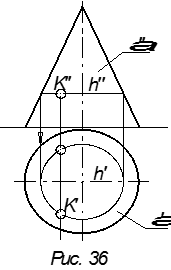
Зная одну проекцию искомой точки K (K′′) на поверхности, совпадающей с проекцией проецирующей прямой, находим её вторую проекцию. Для этого через точку K на поверхности конуса проводим линию особого положения (горизонтальную окружность) (рис.36).
3. Найти точку пересечения линии и плоскости в случае, когда ни прямая, ни поверхность не занимают проецирующего положения.
 Алгоритм решения
задачи
Алгоритм решения
задачи
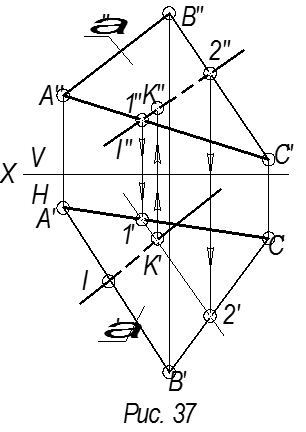
1) Заключить заданную линию L во вспомогательную секущую плоскость γ (след γV).
2) Построить линию пересечения вспомогательной секущей плоскости γ с заданной плоскостью ∆ABC (линия 1-2). Сначала отмечают эту линию на пл. V (линия 1′′-2′′), а затем по линии связи строят горизонтальную проекцию (линия 1′-2′).
3) На пересечении полученной линии 1-2 (1′-2′) с заданной прямой L (L′) находят искомую точку K(K′). По линии связи определяют фронтальную проекцию этой точки (K′′).
4)
 Определяют видимость линии
(рис. 37).
Определяют видимость линии
(рис. 37).
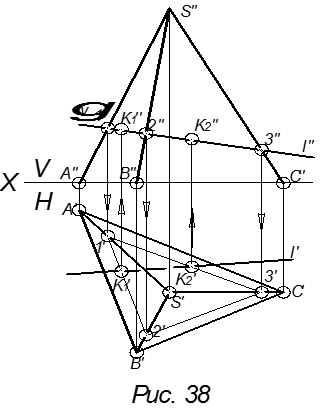
В данном примере (рис. 38) прямую L заключили во вспомогательную проецирующую секущую плоскость γ (γV), которая пересекла грани пирамиды по треугольнику 1-2-3. Далее находят горизонтальную проекцию этого треугольника (1′-2′-3′). На пересечении заданной линии с полученным треугольником, находящемся в одной плоскости с линией L получают искомые точки K1 и K2.
4.
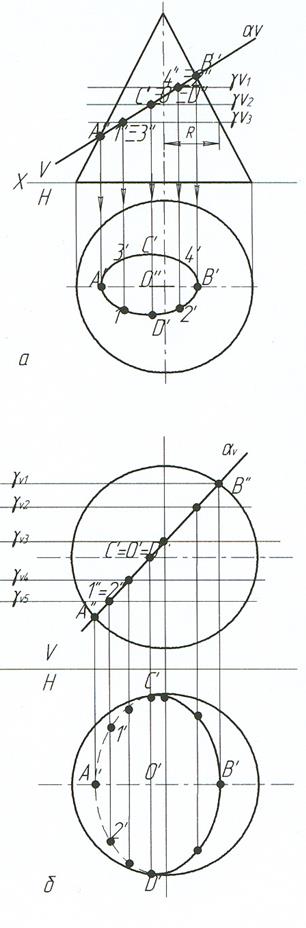 Построить линию пересечения
конуса проецирующей плоскостью α.
Построить линию пересечения
конуса проецирующей плоскостью α.
В этом случае, если плоскость пересекает все образующие конуса, в сечении на поверхности образуется эллипс.
На плоскости V большая ось AB(A′′B′′) и сам эллипс совпадают и проецируются в одну прямую.
|
Горизонтальной проекцией эллипса будет тоже эллипс. Большая ось находится по линии связи. Малая ось проходит через середину большой оси.
На пл. H малую ось находят с помощью вспомогательной горизонтальной секущей плоскости γ2(γV2).
![]()
|
5. Построить сечение сферы проецирующей плоскостью α (рис. 40).
|
большая ось CD (C’D’), а малая ось AB (A’B’). Точки А и В расположены на главном меридиане шара. Точки 1-2 (1’-2’) – видимости эллипса, расположены на экваторе шара.
![]()
![]()
![]() 6. Построить линию пересечения двух поверхностей (конуса и сферы).
6. Построить линию пересечения двух поверхностей (конуса и сферы).
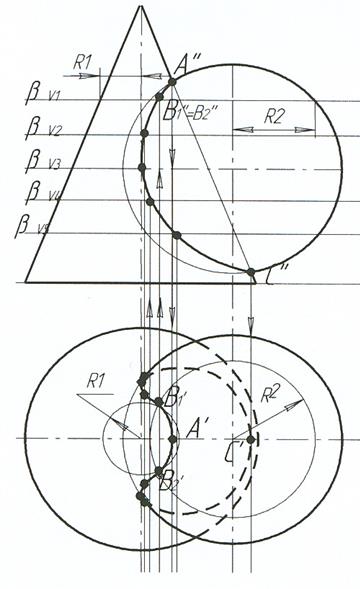
Искомая линия пересечения есть пространственная кривая линия. Её строят по точкам общим для обеих поверхностей конуса и сферы. Для этого используют метод вспомогательных секущих плоскостей β1, β2, β3,… Их вводят так, чтобы они пересекали обе поверхности по простым линиям (по прямой или окружности).
В данном примере (рис. 41) сначала находят так называемые характерные точки A и C. Это уже имеющиеся точки пересечения главного меридиана шара с образующей конуса, находящиеся в одной плоскости.
А далее необходимо:
1) ввести вспомогательную секущую плоскость (например, β1);
2)
|
3) находят точки пересечения полученных линий окружностей сначала на плоскости H (В1 и В2), а затем по линии связи на плоскости V в этой же плоскости β1;
4) этот алгоритм нахождения точек повторяют n раз.
|
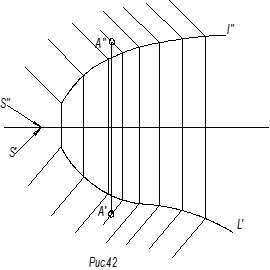
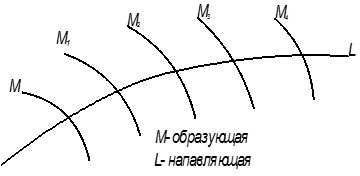 В начертательной геометрии поверхность рассматривается как совокупность
некоторой перемещающейся в пространстве по заданной программе линии. Эта
подвижная линия может оставаться неизменной, а может менять свою форму –
перегибаться или деформироваться, и называется она образующей. Эта образующая
при своем движении скользит по другой неподвижной линии, которая называется
направляющей. Наиболее распространенный способ задания поверхности на чертеже –
кинематический. При этом задаются несколько положений образующей линии и
положение одной или нескольких направляющих (рис.42).
В начертательной геометрии поверхность рассматривается как совокупность
некоторой перемещающейся в пространстве по заданной программе линии. Эта
подвижная линия может оставаться неизменной, а может менять свою форму –
перегибаться или деформироваться, и называется она образующей. Эта образующая
при своем движении скользит по другой неподвижной линии, которая называется
направляющей. Наиболее распространенный способ задания поверхности на чертеже –
кинематический. При этом задаются несколько положений образующей линии и
положение одной или нескольких направляющих (рис.42).
Таким образом поверхность определяют геометрические фигуры (точки, линии, поверхности), с помощью которых могут быть образована поверхность и порядок ее формирования с помощью этих фигур.
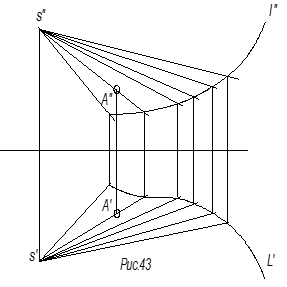
 Образована прямолинейной
образующей, перемещающейся по криволинейной направляющей. При этом образующая
остается параллельной заданному направлению S(рис. 43).
Образована прямолинейной
образующей, перемещающейся по криволинейной направляющей. При этом образующая
остается параллельной заданному направлению S(рис. 43).
![]()
|
|
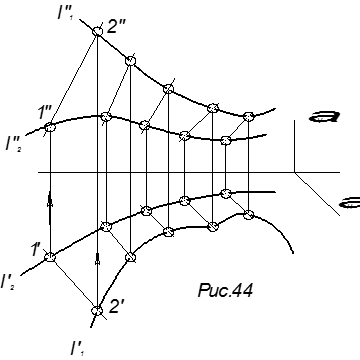
Линейчатые неразвертываемые
поверхности с двумя направляющими
и плоскостью параллелизма
Цилиндроид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.