Начертательная геометрия: Учебное пособие, страница 5

Примером поверхности, задаваемой каркасом, может служить топографическая поверхность (рис.58). Роль каркасных линий здесь выполняют горизонтали поверхности. Расстояния между горизонталями, как правило, берутся одинаковыми на фронтальной проекции. Горизонтальные проекции горизонталей определяются по линиям связи с вертикальными проекциями.

Метрические задачи

Эти задачи делятся на два типа:

1)  задачи на определение расстояния между двумя точками;

2)  задачи на нахождение угла между двумя прямыми.

Определение расстояния

В  общем   случае   на   одной   плоскости   встречаются   следующие   задачи

(рис.59-63):

1.  Определить расстояние от точки до точки.

      А

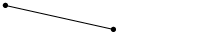
  i.  Рис.59

2.  Определить расстояние между двумя прямыми.

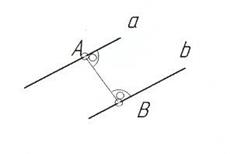Рис.60

3.  Определить расстояние между точкой и прямой.

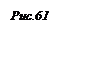
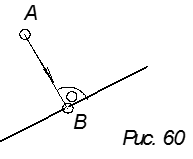4.  Определить расстояние от точки до плоскости.

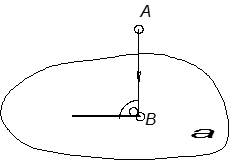
5.  определить расстояние между двумя плоскостями (рис.63).

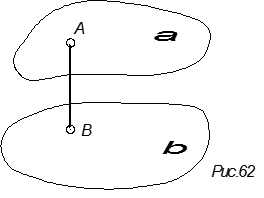
Во всех этих случаях задачи сводятся к определению расстояния от точки одного геометрического образа до точки другого.

6.  Определение углов

В общем случае встречаются следующие задачи (рис.64-68):

1. 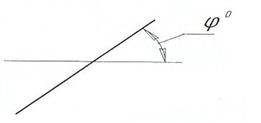 Определить истинную величину угла между двумя прямыми.

2.  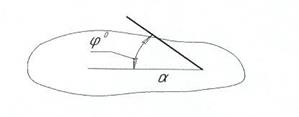Определить истинную величину угла между прямой а и плоско-
стью α.

3.  Определить истинную величину угла между двумя плоскостями α и β.

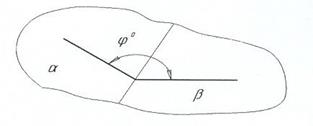
4.  Определить истинную величину угла между двумя кривыми a и b.

а

Рис.67

b

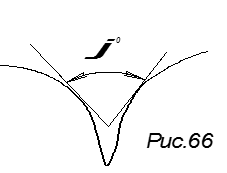
5.  Определить истинную величину угла между двумя криволинейными поверхностями α и β.

	Рис.68

 

                 Во всех этих случаях задачи сводятся к определению величины угла между двумя прямыми. Натуральные величины расстояний и углов определяются путем перевода отрезка или угла в положение, параллельное плоскости проекции, различными способами преобразования чертежа. Наиболее употребительными способами являются способ перемены плоскостей и метод вращения геометрического образа вокруг выбранной определенным образом оси вращения.

Способы преобразования чертежа

Способ перемены плоскостей проекций

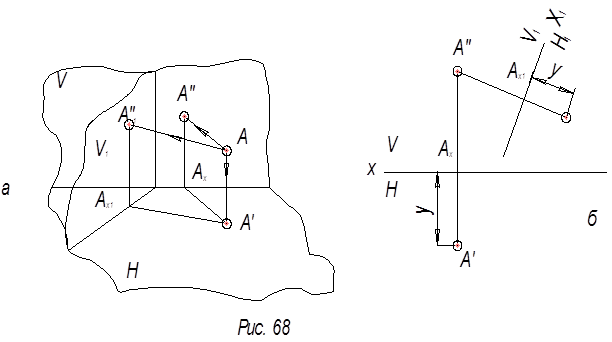
Сущность способа перемены плоскостей проекций заключается в том, что заданные геометрические образы остаются неподвижными, а система плоскостей проекций (старая система) заменяется новой системой двух взаимно-перпендикулярных плоскостей проекций. При этом заменяется одна из плоскостей проекций, а вторая остается. В дальнейшем можно производить нужное количество замен (рис.69).

			б
	Рис.69

При перемене фронтальной плоскости проекций выбираем новую ось проекций (x₁). Из горизонтальной проекции точки проводим прямую, перпендикулярную к новой оси проекции (линии связи) и на этой прямой от новой оси проекций откладываем величину координаты z точки для нахождения новой фронтальной проекции точки (рис.70).

	Рис.70

 

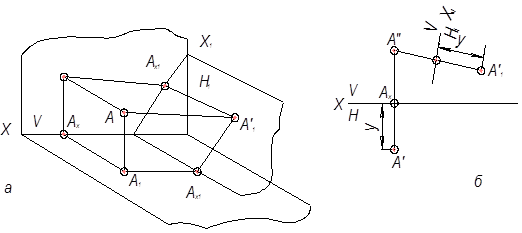
При перемене горизонтальной плоскости проекций выбираем новую ось проекций (x₁). Из фронтальной проекции точки проводим прямую перпендикулярную к новой оси проекций и на этой прямой (линии связи) от новой оси проекций откладываем величину координаты y точки для нахождения новой горизонтальной проекции точки.

Пример 1.

Произвести перемену плоскостей проекций так, чтобы отрезок прямой АВ стал параллельным горизонтальной плоскости проекций (рис. 71).

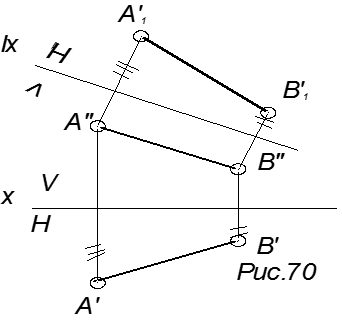
 В этом чертеже новая горизонтальная проекция отрезка (А¢₁В¢₁) есть истинная величина отрезка АВ и расстояния между точками А и В.

Пример 2.

Произвести перемену плоскостей проекций таким образом, чтобы отрезок АВ стал перпендикулярным к новой горизонтальной плоскости проекций (рис. 72).

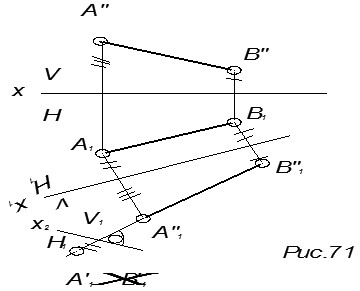
x₁ || A¢B²

                      x₂ ^ A²₁B²₁

Способ вращения вокруг проецирующих прямых и прямых уровня

При вращении геометрического образа (например, точки) вокруг некоторой неподвижной оси, называемой осью вращения, каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения. Эта плоскость называется плоскостью вращения.

При этом точка перемещается по окружности, центр которой расположен на пересечении оси вращения с плоскостью вращения (это центр вращения), а радиус окружности (радиус вращения) равен расстоянию от вращаемой точки до центра вращения.

Пример 1.

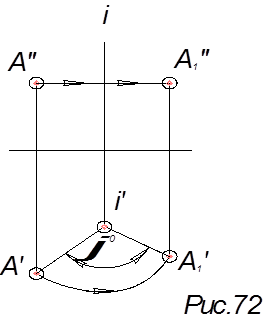
 Повернуть точку А вокруг оси i на угол j°  (рис.73).

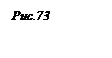
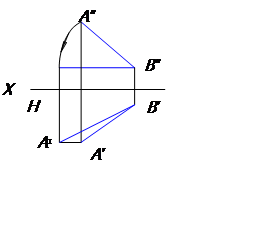
Пример 2.

Отрезок прямой АВ повернуть вокруг оси i так, чтобы он стал параллельным плоскости Н (рис.74).

 A²₁B² || x

                    AB || H

A¢₁B¢ ­– натуральная величина отрезка AB

	Рис.74

 

Определение расстояний между двумя точками

Пример 1

Определить расстояние между точками А и В.

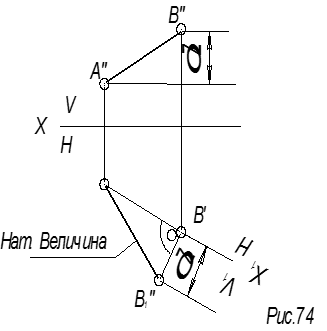Соединить точки А и В.  Найти натуральную величину  отрезка АВ способом прямоугольного треугольника. Этот способ является упрощенной схемой способа перемены плоскостей проекций. Переводим отрезок АВ в положение, параллельное какой-либо плоскости проекций  (в данном примере || пл. V₁), (рис.75).

Пример 2

Определить расстояние от точки до плоскости.

Признак перпендикулярности прямой и плоскости.

Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, принадлежащим плоскости.