Применение математических моделей в психолого-педагогическом исследовании

Даты занятий по ППП   52 гр. 08-09 уч. г. :

1.      02.09.08                2.  02.09.08            3.  03.09. 

4.      09.09.08                5.  09.09.08            6.  10.09.08.           7.     10.09.08

8..    16.09.08                 9.  16.09.08            10.  17.09.08

11.    23.09.08               12.  23.09.08           13.   24.09.08         14.     24.09.08    

15.    30.09.08               16.    30.09.08         17.  01.10.08

18.    07.10.08               19. 07.10.08             20.  08.10.08           21.     08.10.08

22.    14.10.08               23.  14.10.08           24.    15.10.08.  

25.    21.10.08              26.  21.10.08.           27.   22. 10.08           28.     22.10.08.

Экзамен.

Задачи по теме 6: МАТЕМАТИЧЕСКИЕ МОДЕЛИ, МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 

2. Применение математических моделей в психолого-педагогическом исследовании. Пример основан на материалах реального психолого-педагогического исследования. Расчеты приведены частично и лишь на начало формирующего эксперимента.

Массив формирующего эксперимента – 100 человек: 52 учащихся  из двух экспериментальных вторых классов (ЭК_1,  ЭК_2,) и 48 учащихся из двух контрольных вторых классов (КК_1,  КК_2,). Цель формирующего эксперимента – проверить гипотезу о благоприятном влиянии на эмоциональное здоровье учащихся обучения, основанного на  образовательной технологии, характеризующейся тем, что: а) в цели обучения учебному предмету включены цели здоровьесбережения; б) содержание раскрывает гуманитарные аспекты предметного знания; в) обучение строится на специальных группах методических средств, включающих и группу средств здоровьесбережения. Длительность формирующего эксперимента – один учебный год.

Результаты    экспериментального    обучения    отслеживались  по  состоянию на начало и по окончании формирующего эксперимента: а) предметной подготовки; б) здоровья школьников (эмоционального и физического).

Здесь представлены некоторые математические методы обработки результатов исследования влияния обучения учебному предмету только на эмоциональное здоровье учащихся. Оно отслеживалось с помощью теста школьной тревожности Филлипса[1], адаптированного применительно к обучению учебному предмету. Тестирование проводилось в первую неделю учебного года и в конце учебного года. При обработке результатов подсчитывалось число несовпадений ответов с ключом, данным в тесте по каждому из 8 факторов тревожности. Уровень тревожности определялся в соответствии с принятой по этому тесту градацией: меньше 50% несовпадений – нормальная тревожность, более 50% – повышенная тревожность, более 75% – высокая тревожность.

Результаты для одной пары экспериментальных и контрольных классов представлены на полигонах частот (рис. 17). Для второй пары представление аналогично.

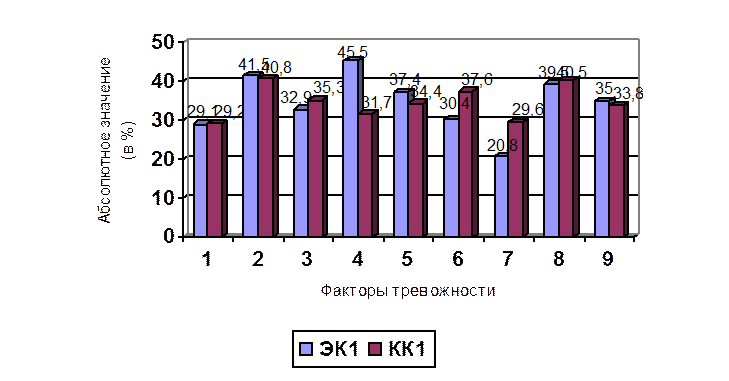
Уровень школьной тревожности (по Филипсу) учащихся ЭК₁  и КК₁ на начало формирующего эксперимента

Рис. 17

Для определения достоверности различий между экспериментальными и контрольными классами применим к полученным результатам t – критерий Стьюдента,  вычисленный по формуле для равночисленных выборок: 

 =     

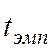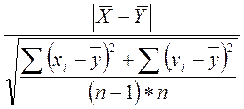
Все условия t – критерия Стьюдента выполнены: выборки учащихся несвязные и распределены по нормальному закону. В обоих случаях подсчет числа степеней свободы осуществляется по формуле k = (n₁ - 1) + (n₂ - 1) = n₁ + n₂ – 2, поэтому в обоих случаях k = 48. Результаты вычислений отражены в таблице.

Таблица 1

	Факторы школьной тревожности
	1	2	3	4	5	6	7	8	9 Общее
ЭК1	29,2	41,5	32,9	45,5	37,4	30,4	20,8	39,5	35
КК1	29,2	40,8	35,3	31,7	34,4	37,6	29,6	40,5	33,8
t эмп1	0	0,15	0,56	1,85	0,43	1,13	0,97	0,23	0,28
ЭК2	27,1	37,4	33,4	35,8	41	33,3	15,6	34,7	32,4
КК2	30,7	39,6	34,7	34,8	36,2	27,8	10,4	31	26,8
t эмп1	0,63	0,47	0,32	0,15	0,27	0,20	0,28	0,16	0,12

Сформулируем нулевую гипотезу  H₀ : различия между показателями уровня тревожности имеют лишь случайный характер; альтернативную гипотезу H₁ – разница между показателями в экспериментальных и контрольных классах имеет не случайные различия.H_{1 :}  различия между показателями уровня тревожности носят не случайный характер, они статистически значимы.

Сравнив t _эмп1  для ЭК1 и КК1, ЭК2 и КК2 обнаруживаем, что t _эмп1  <t _кр, что позволяет отклонить гипотезу H₁ и принять нулевую гипотезу H₀ – разница между показателями в экспериментальных и контрольных классах на начало формирующего эксперимента имеет лишь случайные различия. Это подтверждает, что на входном контроле уровень школьной тревожности детей экспериментальных и контрольных классов примерно одинаков и все значения меньше 50%, что говорит о нормальной тревожности на начало учебного года, т. е. без влияния учебного процесса. По окончании экспериментального обучения вновь определялись показатели школьной тревожности и аналогичным образом определялась статистическая значимость различий в показателях экспериментального и контрольного классов. Существуют и другие математические модели для оценки результатов педагогического эксперимента.  

Задачи по теме 9: ТЕОРИЯ ВЕРОЯТНОСТЕЙ  

1. В тестовом задании нужно выбрать все правильные ответы из  5-ти данных. а) Какова вероятность «угадывания» правильного выбора, если студент не знает, сколько правильных ответов среди предложенных, но знает, что хотя бы один ответ правильный, и хотя бы один ответ неправильный; а составители заложили в это задание 2 правильных ответа? б) Какова вероятность угадывания одного правильного ответа?

2. Дано: АВ = 16 см, АС = 3 см, СD = 4 см. На отрезке АВ случайным образом отмечается точка Х. Какова вероятность того, что точка Х попадет на отрезок: 1) АC   2) АD   3) СD  4) CВ  5) АВ?

3. Расположите  события в порядке возрастания вероятностей (в случае равенства вероятностей запишите в порядке возрастания номера событий):

Из урны, в которой лежат 12 шаров, пронумерованных числами от 1 до 12, наугад извлекают два шара.

А:  сумма чисел и произведение чисел простые числа;

Б:  сумма чисел кратна 8;

В: сумма чисел кратна 5, а произведение чисел четное число;

Г: сумма чисел не больше 12.

4. Из коробки, в которой находится 7 красных и 5 синих шаров, случайно выкатились 4 шара. Какова вероятность того, что среди выкатившихся шаров больше трех красных?

5. Из набора домино случайным образом вынули 2 костяшки.  Найти вероятность того, что это  2) не костяшки, содержащие шестерки; 1) не костяшки «0 - 3» и «0-2».