Применение математических моделей в психолого-педагогическом исследовании, страница 4

Табл. 2

Данные диагностики по окончании экспериментального обучения

Студенты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	всего
Баллы	20	26	28	29	30	24	19	20	16	20	26	20	25	27	28	24	18	18	28	22

Решение.

Выполнять будем в последовательности, данной в задании.

Построить статистический (вариационный, упорядоченный) ряд, интервальный ряд, статистическое распределение, полигон частот и гистограмму; найти (вычислить) моду, медиану, разброс, среднее арифметическое (математическое ожидание ), дисперсию, среднее квадратическое, среднее квадратическое отклонение.

Выполним эти две части задания вначале для данных до начала экспериментального обучения, а затем для данных по его окончании. 

Характеристики результатов статистического наблюдения

до экспериментального обучения (по таблице 1)

Статистический ряд  (изменены номера диагностируемых студентов) до начала экспериментального обучения       

Студенты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	Всего
Баллы	14	16	16	17	17	18	18	18	18	18	20	20	24	25	27	27	27	28	28	28	424	≈ 21,2

Статистическое распределение

Баллы	14	16	17	18	20	24	25	27	28
Частота	1	2	2	5	2	1	1	3	3
Относительная частота	1/20	2/20	2/20	5/20	2/20	1/20	1/20	3/20	3/20
Процентная частота	5 %	10 %	10 %	25 %	10 %	5 %	5 %	15%	15%

Разброс (размах)  14 . 

Интервальный ряд. Для построения интервального ряда учтем, какое количество баллов можно было набрать, а также найдем в таблице  наименьшее количество баллов и наибольшее, определим разброс и затем зададим интервалы, которые могут быть интерпретированы в соответствии с целями исследования и целями диагностики. Например, выделив для данной задачи интервалы в 5 баллов получим 4 интервала, которые могут быть интерпретированы как показатели наличия у испытуемых какого-либо качества разного  уровня: 10 – 15 баллов – низкий, 15 – 20 баллов – ниже среднего, 20 – 25 баллов – средний, 25 – 30 баллов – высокий.

Мах. – 28. Мin. 14

Интервальный ряд.

Уровни	Низкий	Ниже среднего	Средний	Высокий
Баллы	10 – 15	15 – 20	20 – 25	25 – 30
Количество студентов	1	11	2	6
Относительная частота	1/20	11/20	2/20	6/20
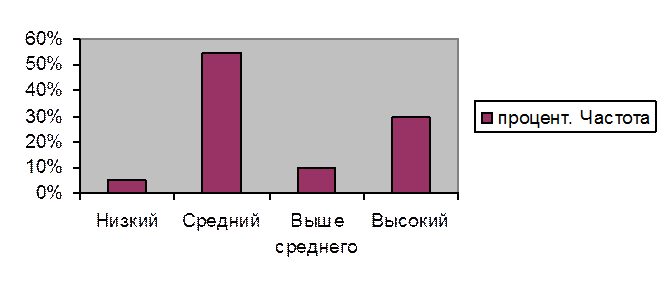
Процентная частота	5 %	55 %	10 %	30 %

Полигон частот.

Результаты диагностики до начала экспериментального обучения

Гистограмма

Результаты диагностики до начала экспериментального обучения

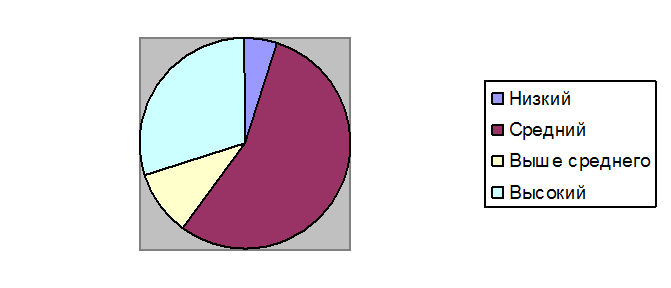
Мода   Мо = 18

Медиана   Ме = (18 + 20) : 2 = 19. (определяется по статистическому ряду как среднее арифметическое 10-го и 11-го значений, так как объем выборки – 20 значений, четное число.  Для нечетного числа медиана -  это значение середины статистического ряда.

Разброс (размах) – разность между наименьшим и наибольшим значениями вариант: Мах. – 28. Мin. 14. размах = 28 – 14 = 14. 

Среднее арифметическое ( математическое ожидание - ожидаемое среднее значение случайной величины). Обозначается М(Х),   m_x  или  (занесено в последний столбец таблицы 1).

М(Х) ≡ m_x ≡ =

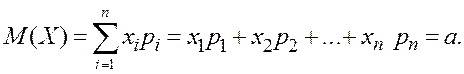
По данным решаемой задачи среднее арифметическое удобно подсчитать по таблице статистического распределения:  

 = (14 • 1 + 16 • 2  + 17 • 2 + 18 • 5 + 20 • 2 + 24 • 1 + 25 • 1 + 27 • 3 + 28 • 3) : 20 = 424 : 20 ≈ 21,2. 

Дисперсия (статистическая дисперсия):

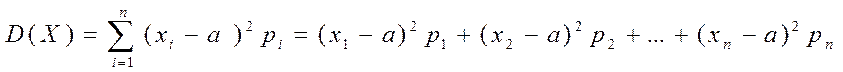, где  а – среднее арифметическое,  х_i – середина интервала или значение варианты, n – число различных значений выборки, р_i – относительная частота .

D (X) = (14 – 20)²  • 1/20 + (16 – 20)² • 2/20  + (17 – 20)² • 2/20  + (18 – 20)² • 5/20  + (20 – 20)² • 2/20 + (24 – 20)² • 1/20 + (25 – 20)² • 1/20 + (27 – 20)² • 3/20 + (28 – 20)² • 3/20 =

= 6² • 1/20 + 4² • 2/20 + 3² • 2/20 + 2² • 5/20 + 0² • 2/20 + 4² • 1/20  + 5² • 1/20  + 7² • 3/20 + 8² • 5/20  3 =

= 36/20 + 32/20 + 18/20 + 20/20 + 0/20 + 16/20 + 25/20 + 147/20 + 320/20 =

= 30,7

статистическое среднеквадратическое отклонение 

   ≈ 5,54 

Характеристики результатов статистического наблюдения

до экспериментального обучения (по таблице 2)

Статистический ряд  (изменены номера диагностируемых студентов) по окончании экспериментального обучения       

Студенты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	Всего
Баллы	16	18	18	19	20	20	20	20	22	24	24	25	26	26	27	28	28	28	29	30		24,35

Статистическое распределение