Применение математических моделей в психолого-педагогическом исследовании, страница 5

Баллы	16	18	19	20	22	24	25	26	27	28	29	30
Частота	1	2	1	4	1	2	1	2	1	3	1	1
Относительная частота	1/20	2/20	1/20	4/20	1/20	2/20	1/20	2/20	1/20	3/20	1/20	1/20
Процентная частота	5 %	10 %	5 %	20 %	5 %	10 %	5 %	10%	5%	15 %	5 %	5 %

Интервальный ряд

Уровни	Низкий	Средний	Выше среднего	Высокий
Баллы	10 – 15	15 – 20	20 – 25	25 – 30
к-во студентов	0	7	4	9
Отн. частота	0	7/20	4/20	9/20
Процент. частота	0 %	35 %	20 %	45 %

Интервальный ряд (для компьютерного построения полигона частот)

Уровни	Низкий	Ниже среднего	Средний	Высокий
Процент. частота	0 %	35 %	20 %	45 %

Полигон частот

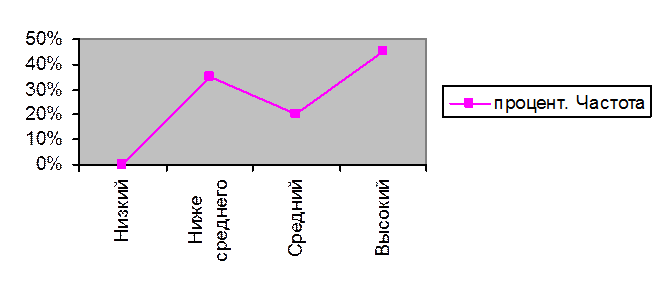
Гистограмма по результатам диагностики

по окончании экспериментального обучения

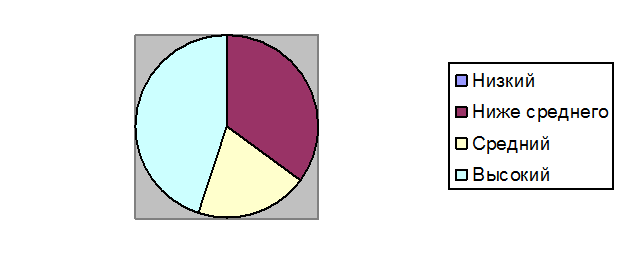
Мода   Мо = 20

Медиана   Ме = (24 + 24) : 2 = 24. (определяется по статистическому ряду как среднее арифметическое 10-го и 11-го значений, так как объем выборки – 20 значений, четное число.  Для нечетного числа медиана -  это значение середины статистического ряда.

Разброс (размах) – разность между наименьшим и наибольшим значениями вариант: Мах. – 28. Мin. 14. размах = 30 – 16 = 14. 

Среднее арифметическое (математическое ожидание - ожидаемое среднее значение случайной величины). Обозначается М(Y),   m_x  или  (занесено в последний столбец таблицы 1). р - частота

М(Х) ≡ m_x ≡ =

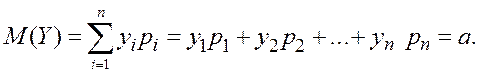
По данным решаемой задачи среднее арифметическое удобно подсчитать по таблице статистического распределения: 

 = (16 • 1 + 18 • 2  + 19 • 2 + 20 • 4 + 22 • 1 + 24 • 2 + 25 • 1 + 26 • 2 + 27  1 + 28 • 3 + 29 • 1 + 30 • 1) : 20 = 487 : 20 = 24,35. 

Дисперсия (статистическая дисперсия):

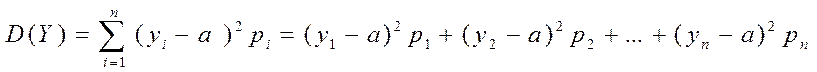,  где  а – среднее арифметическое, y_i – середина интервала или значение варианты, n – число различных значений выборки,  р_i – относительная частота .

D (Y) = (16 – 20)²  • 1/20 + (18  – 20)² • 2/20  + (19 – 20)² • 1/20  + (20 – 20)² • 4/20  + (22 – 20)² • 1/20 + (24 – 20)² • 2/20 + (25 – 20)² • 1/20 + (26 – 20)² • 2/20 +  (27 – 20)² • 1/20 + (28 – 20)² • 3/20 + (29 – 20)² • 1/20 + (30 – 20)² • 1/20 = 16/20 + 8/20 + 1/20 + 4/20 + 32/20 + 25/20 + 72/20 + 49/20 + 204/20 + 81/20 + 100/20 =  592/20 = 29,6

Статистическое среднеквадратическое отклонение 

   ≈ 5, 45

Сравнение результатов диагностики до начала экспериментального обучения и по его окончании с помощью t – критерия Стьюдента

Для сравнения полученных результатов, применив t – критерий Стьюдента сформулируем гипотезы: нулевая гипотеза H₀ – разница между показателями до экспериментального обучения и после такого обучения имеет лишь случайные различия; альтернативная гипотеза H₁ – разница между показателями до экспериментального обучения и после такого обучения имеет не случайные различия. Для равночисленных выборок Д₁ и Д₂   =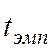

 ≈  ;

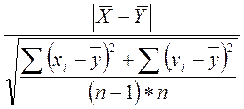
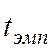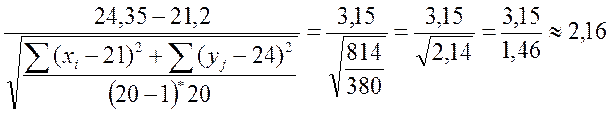где n = (20 – 1) + 20  = 39

Для Д1 и Д2 t эмп2 = 2,16  >

t кр = 2,01

для Р ≤ 0,05.

Вспомогательные таблицы для вычисления t – критерия Стьюдента

Студенты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	Всего
Баллы	14	16	16	17	17	18	18	18	18	18	20	20	24	25	27	27	27	28	28	28	424	≈ 21,2
|xi  –  |	7	5	5	4	4	3	3	3	3	3	1	1	3	4	6	6	6	7	7	7		≈ 21
|xi  –  |2	49	25	25	16	16	9	9	9	9	9	1	1	9	16	36	36	36	49	49	49	458

Студенты	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	Всего
Баллы	16	18	18	19	20	20	20	20	22	24	24	25	26	26	27	28	28	28	29	30		24,35
|yj  – |	8	6	6	5	4	4	4	4	2	0	0	1	2	2	3	4	4	4	5	6		≈ 24
|yj  – |2	64	36	36	25	16	16	16	16	4	0	0	1	4	4	9	16	16	16	25	36	356

ВЫВОД. Так как t _эмп2  больше  t _кр, то гипотеза H₀ отклоняется и принимается гипотеза H₁ . Это означает, что разница между показателями до экспериментального обучения и после такого обучения имеет не случайные различия.

Следовательно, подтверждена и гипотеза экспериментального исследования.