Методичні вказівки до лабораторних робіт з дисципліни "Матеріали мехатронних пристроїв", страница 24

Величину, зворотну питомій провідності У, яку називають питомим спротивом , для провідника з постійним поперечним діленням S і довжиною I можна обчислити за формулою:

                                                       ,                                                (6.1)

де R – спротив провідника.

Для зміни питомого електричного спротиву на практиці користуються зовнішньо системною одиницею Ом*мм / м.

Ефект, що спостерігається, є можливістю металів створювати спротив проходженню електричного току і залежить від їхньої фізичної природи, а величина питомого спротиву металічного провідника може бути визначена за наступною формулою:

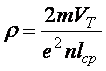                                                         ,                                       (6.2)     

де m – маса електрона;

     V – середня швидкість теплового руху електрона всередині металічного провідника;

      – середня довжина вільного пробігу електрона.

Розсіяння, яке призводить до появи спротиву, виникає в тих випадках, коли в решітці різного виду є порушення її правильної будови, тобто дефекти структури. Дефекти структури можуть бути статичними, динамічними, атомними (точечними), протяжними. Однак і в чистих металах із удосконаленою структурою є ефект спротиву вільного руху електронів. І причиною такого ефекту є теплові коливання атомів у вузлах кристалічної решітки. Звідси стає зрозумілим, що зі збільшенням температури збільшується амплітуда коливань атомів і пов’язані з ними флуктуації періодичного поля решітки. А це, в свою чергу, посилює розсіювання електронів і викликає зростання питомого спротиву.

Електричний спротив матеріалу, обумовлений тепловим ефектом, позначити .

Для характеристики залежності відносної зміни питомого спротиву матеріалу від температури ввели поняття температурного коефіцієнта питомого спротиву .

У діапазоні температур, де залежність питомого спротиву р від температури Т близька до лінійної, допустима лінійно-кусочна апроксимація цієї залежності, і величина питомого спротиву в кінці діапазону температури Т може бути підрахована за формулою:

                                                   ,                               (6.3)

де  - питомий спротив на початку діапазону температур. Величину називають середнім температурним коефіцієнтом питомого спротиву в даному діапазоні температури:

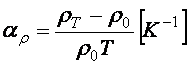                           .                                 (6.4)

Диференційне вираження для має вигляд:

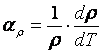                                                   .                                     (6.5)

Позитивний знак відповідає випадку, коли питомий спротив у периферії даної точки збільшується при підвищенні температури. Величина також є функцією температури. В області лінійної залежностівід Т справедливий вираз:

                                             ,                        (6.6)