Методичні вказівки до лабораторних робіт з дисципліни "Матеріали мехатронних пристроїв", страница 13

	а)

 

прикладеної до конденсатора напруги існує нелінійна залежність, яка характерна для сегнетоелектриків, то на екрані осцилографа з’являється петля діелектричного гістерезиса (рис. 4.2б). Величина вмісткості в цих випадках визначається за відношенням амплітудного значення Q_xm до амплітудного значення U_xm:

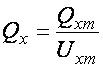                                                                                                     (4.2)  

                                                                                                     

Значення вмісткості, яке знайдене за формулою для нелінійних конденсаторів, носить назву ефективної вмісткості.

Площа петлі гістерезиса у визначеному масштабі дає значення активної енергії W, яку вживає конденсатор за один період:

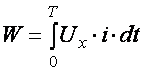                                                           _,                                               (4.3) 

де і  – миттєві значення напруги і току.

Миттєві значення напруги на конденсаторі С₀ вимірюється вертикальним відхиленням променя Y, помноженому на масштаб вертикального відхилення:

.                      (4.4)

Разом із тим:

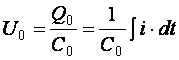                                                  ,                              (4.5)         

Прирівнюючи праві частини (2.4) і (2.5 ), після диференціювання отримуємо:

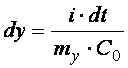                                                     .                                    (4.6)    

Аналогічно (1.4) визначається миттєве значення напруги на :

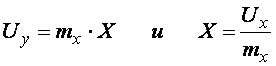                                            .              (4.7)

Елемент площі петлі гістерезиса (рис. 2.2 б) з урахуванням (2.6) і (2.7):

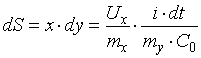                                             .                              (4.8)

Вся площа гістерезиса:

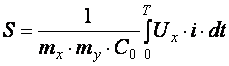                                                ;                      (4.9)

                                                   ,                          (4.10)

Якщо і виражається в см, S - см², С₀ – в фарадах, то W в Джоулях.

Потужність втрат у конденсаторі:

                           ,                          (4.11)