Специальная теория относительности, страница 8

Масса   является инвариантом, следовательно, и выражение (6.10) представляет собой инвариант, т.е. имеет одинаковую величину во всех инерциальных системах отсчета. Сами по себе величины E и не являются инвариантами, так как они зависят от скорости, которая меняется при переходе из одной системы отсчета в другую.

     Будем считать, что частица движется параллельно оси x, в системе скорость частицы равна . Тогда согласно релятивистской теореме сложения скоростей скорость в системе Xравна

           (6.11)

Здесь - скорость, с которой система движется относительно системы X. Энергию в системе X выразим через . Для этого вычислим выражение  :

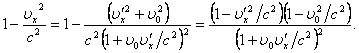
Тогда энергия

Полученная формула справедлива при любой взаимной ориентации векторов и . Это означает, что в преобразованиях участвует только компонента импульса . Так как , выражение для импульса принимает вид =.

Подставим в него из (6.11), имеем

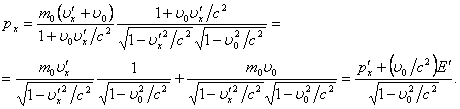
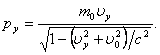Теперь будем считать, что в системе  частица движется параллельно оси и, следовательно, . В системе X компонента скорости частицы по оси x равна , так что . Соответственно,  Так как  , то из преобразований  Лоренца для скоростей , и

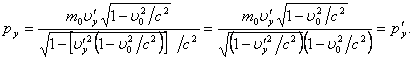
Аналогичный результат получается для компоненты . Тогда преобразования для энергии и импульса принимают вид:

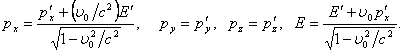
Эти формулы совпадают с формулами (6.2) преобразования координат и времени.

     По аналогии с трехмерными векторами в евклидовом пространстве можно определить четырехмерные векторы. Под четырехмерным вектором понимают совокупность  четырех величин  преобразующихся по тем же формулам, что и ct, x,y, z. Квадрат такого вектора равен . Вследствие того, что компоненты преобразуются так же, как координаты, квадрат четырехмерного вектора оказывается  инвариантным по отношению к преобразованиям Лоренца. Тогда совокупность величин  образует четырехмерный вектор, называемый вектором энергии-импульса. Квадрат этого вектора является инвариантом и равен