![]()
![]()
Длина
линейки в штрихованной системе (длина покоящейся линейки) равна ![]() . Чтобы наблюдатель
. Чтобы наблюдатель ![]() правильно измерил в своей системе
отсчета длину движущегося предмета, он должен постараться отметить положения
концов линейки в моменты времени, которые он считает совпадающими:
правильно измерил в своей системе
отсчета длину движущегося предмета, он должен постараться отметить положения
концов линейки в моменты времени, которые он считает совпадающими: ![]() , поэтому
, поэтому ![]() .
Очевидно,
.
Очевидно, ![]() - длина линейки, которую измерит
наблюдатель X. Относительно этого наблюдателя линейка движется со
скоростью
- длина линейки, которую измерит
наблюдатель X. Относительно этого наблюдателя линейка движется со
скоростью ![]() . Тогда
. Тогда ![]() ,
или
,
или ![]() - длина движущейся линейки в
- длина движущейся линейки в ![]() раз меньше длины этой же линейки в покое. Данный факт
получил название лоренцева сокращения длины.
раз меньше длины этой же линейки в покое. Данный факт
получил название лоренцева сокращения длины.
6.4.ОДНОВРЕМЕННОСТЬ СОБЫТИЙ В РАЗНЫХ СИСТЕМАХ ОТСЧЕТА
То, что один наблюдатель считает метровую линейку короче, чем другой, с точки зрения физики объясняется несовпадением для них понятия одновременности, т.е. события, одновременные для одного наблюдателя, не являются таковыми для другого. При этом следует помнить, что для измерения длины метровой линейки положения обоих ее концов следует отмечать одновременно.
Рассмотрим движущийся
вагон (рис.6.5) и покажем, что события одновременные с точки зрения
неподвижного наблюдателя, не будут одновременными для наблюдателя внутри
вагона. Длина вагона в состоянии покоя равна ![]() для
наблюдателя
для
наблюдателя ![]() , стоящего в центре вагона.
, стоящего в центре вагона.
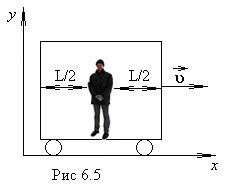 Предположим, что в момент времени
Предположим, что в момент времени ![]() наблюдатель
наблюдатель
![]() проезжает мимо наблюдателя X, который стоит рядом с железнодорожным полотном. В это
время (по часам наблюдателя X) две молнии ударяют в концы вагона и оставляют следы
на рельсах (рис.6.5). Наблюдателю X это дает хорошую возможность измерить длину
проезжает мимо наблюдателя X, который стоит рядом с железнодорожным полотном. В это
время (по часам наблюдателя X) две молнии ударяют в концы вагона и оставляют следы
на рельсах (рис.6.5). Наблюдателю X это дает хорошую возможность измерить длину ![]() вагона как расстояние между
отметками, при этом
вагона как расстояние между
отметками, при этом ![]() .
.
Однако наблюдатель ![]() считает, что молния ударила
сначала в правый конец, действительно, наблюдатель в вагоне движется навстречу
свету от правой молнии и видит раньше этот свет. Если лицо наблюдателя
считает, что молния ударила
сначала в правый конец, действительно, наблюдатель в вагоне движется навстречу
свету от правой молнии и видит раньше этот свет. Если лицо наблюдателя ![]() раньше освещается светом справа, то
это означает, что свет справа достиг его раньше, и этот факт не зависит от
наблюдателя. Но по мнению наблюдателя
раньше освещается светом справа, то
это означает, что свет справа достиг его раньше, и этот факт не зависит от
наблюдателя. Но по мнению наблюдателя ![]() ,
обе вспышки молнии произошли на одинаковом расстоянии от него, и если он
сначала видел вспышку справа, то он и считает, что она произошла раньше, Если
ввести еще одного наблюдателя
,
обе вспышки молнии произошли на одинаковом расстоянии от него, и если он
сначала видел вспышку справа, то он и считает, что она произошла раньше, Если
ввести еще одного наблюдателя ![]() , который начал
двигаться из той же точки не вправо, а влево, то для него раньше произойдет
левая вспышка.
, который начал
двигаться из той же точки не вправо, а влево, то для него раньше произойдет
левая вспышка.
Таким образом, если промежуток времени между двумя событиями короче того времени, которое необходимо для распространения света между ними, то порядок следования этих событий остается неопределенным: он зависит от скорости наблюдателя. В таких случаях может оказаться, что будущее событие опережает предыдущее, если выбрать подходящего движущегося наблюдателя.
6.5. ИНТЕРВАЛ
Вернемся к понятию интервала между событиями. В нештрихованной системе отсчета
квадрат интервала равен ![]() . Будем считать,
что оба события происходят с одной и той же частицей. Тогда
. Будем считать,
что оба события происходят с одной и той же частицей. Тогда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.