Специальная теория относительности, страница 2

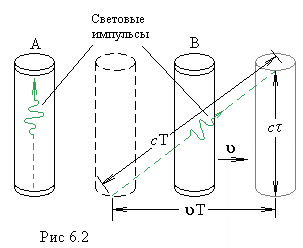
     Рассмотрим наблюдателя   (рис.6.2). Ему путь светового луча от одного края часов   до другого будет представляться более длинным, чем в часах   (световой импульс относительно наблюдателя  движется по диагонали со скоростью света ). Следовательно, с точки зрения наблюдателя  световому импульсу в часах  понадобится больше времени для того, чтобы достичь верхнего зеркала, чем световому импульсу в часах  . Обозначим этот больший промежуток времени , тогда длина диагонали равна , и по теореме Пифагора , отсюда

.

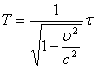В теории относительности множитель, стоящий перед , встречается очень часто и обозначается .

Наблюдатель  видит тиканье часов   через время  , а тиканье своих часов  через время  . Таким образом, любой наблюдатель обнаруживает замедление хода движущихся часов в  раз по сравнению с точно такими же, но находящимися в покое часами. Величина   называется собственным временем. Это измеренный наблюдателем промежуток времени между двумя событиями, которые наблюдатель видит  в одной и той же точке пространства.  Тогда   - промежуток времени между теми же событиями, но измеренный движущимся наблюдателем по его собственным часам. Собственное время  – это время, измеренное наблюдателем, движущимся вместе с часами. Оно одинаково во всех инерциальных системах отсчета, т.е. является инвариантом.

Теория относительности Эйнштейна приводит к взаимосвязи пространства и времени. Эта взаимосвязь состоит в образовании единого пространства-времени, т.е. четырехмерного пространства, по трем осям которого откладывают пространственные координаты x,y,z, а по четвертой – временную координату . Какое-либо событие характеризуется местом  x,y,z, и временем , когда оно произошло. Таким образом, событию отвечает в четырехмерном пространстве точка с координатами  (x,y,z,ct). Эту точку называют мировой точкой.

         Итак, пространство и время являются частями единого целого. Однако время качественно отличается  от пространства. Это проявляется в отличии четырехмерного пространства от обычного трехмерного. В трехмерном пространстве используется евклидова метрика, и квадрат расстояния между точками .

Квадрат расстояния между двумя мировыми точками называется интервалом и равен

 Это пространство является псевдоевклидовым.

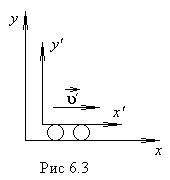
6.2. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА