Специальная теория относительности, страница 6

     Для любой мировой точки B,  лежащей в абсолютно прошедшей области, , т.е. интервал  -времениподобный, однако  и во всех системах отсчета событие B предшествует событию О.

     Для любого события C или D, мировая точка которого лежит в абсолютно удаленных областях, , и интервалы  и  - пространственноподобные. В любой системе отсчета события O и C, или O и D происходят в разных точках пространства. Понятие одновременности этих событий является относительным. В одних системах отсчета событие C (или D) происходит позже, а в других раньше события O. Имеется одна система отсчета, в которой событие C(или D) происходит одновременно с O).

          6.6. ПРЕОБРАЗОВАНИЕ И СЛОЖЕНИЕ СКОРОСТЕЙ

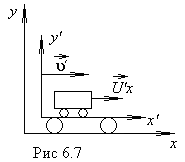     Рассмотрим движение материальной точки (рис.6.7). В системе X положение точки определяется в каждый момент времени t координатами x,y,z. Выражения  представляют собой проекции вектора скорости точки на соответствующие оси в системе отсчета X. В системе положение материальной точки характеризуется  в каждый момент времени координатами  Проекции вектора скорости относительно  на эти оси  определяются выражениями  . Из формул (6.2) получаем

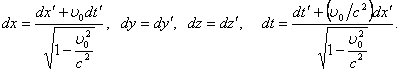
Разделив первые три равенства на четвертое, получаем формулы для преобразования скоростей при переходе их одной системы отсчета в другую:

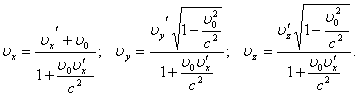      (6.3)

При эти соотношения переходят в преобразования Галилея в классической механике. Обратные преобразования имеют вид:

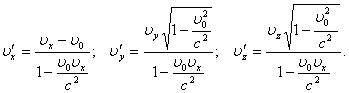
Если тело движется  параллельно оси x, его скорость относительно системы  X совпадает с , а скорость относительно системы  - с . В этом случае закон сложения скоростей принимает вид

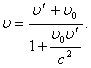             (6.4)

Если скорость частицы в одной системе отсчета =c, то в другой системе, согласно (6.4) эта скорость равна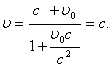

Мы получили, что скорость света одинакова во всех инерциальных системах отсчета.

          6.7. ПРЕОБРАЗОВАНИЯ ДЛЯ ИМПУЛЬСА И ЭНЕРГИИ

      Уравнения Ньютона инвариантны по отношению к преобразованиям Галилея. Однако к преобразованиям Лоренца они оказываются неинвариантными. В частности, не инвариантен к преобразованиям Лоренца вытекающий из законов Ньютона закон сохранения импульса.

     В теории относительности импульс, как и в Ньютоновской механике, равен произведению массы тела на его скорость

                            (6.5)