Рассмотрим
двух наблюдателей, движущихся с относительной скоростью ![]() (рис.6.3).
Один наблюдатель
(рис.6.3).
Один наблюдатель ![]() ,
другой
,
другой ![]() . Наблюдатель
. Наблюдатель ![]() находится в системе координат
находится в системе координат ![]() , а наблюдатель
, а наблюдатель ![]() - в системе
- в системе ![]() .
Назовем эту систему штрихованной. Необходимо найти такие уравнения
преобразования координат, чтобы тело, движущееся со скоростью
.
Назовем эту систему штрихованной. Необходимо найти такие уравнения
преобразования координат, чтобы тело, движущееся со скоростью ![]() в нештрихованной системе, двигался
бы в штрихованной системе с той же скоростью, т.е. если x=ct,
то
в нештрихованной системе, двигался
бы в штрихованной системе с той же скоростью, т.е. если x=ct,
то ![]() . Общий вид преобразования координат
. Общий вид преобразования координат
![]() (6.1)
(6.1)
где ![]() -
некоторые функции скорости.
-
некоторые функции скорости.
Будем считать, что в
начальный момент времени ( при ![]() ) начала координат
обеих систем совпадали, а движение происходит в направлении оси
) начала координат
обеих систем совпадали, а движение происходит в направлении оси ![]() , поэтому
, поэтому ![]() .
.
Рассмотрим часы, которые
находятся в точке ![]() , время между их
“тиканьями” составляет
, время между их
“тиканьями” составляет![]() . Наблюдатель X
видит движущиеся часы, время между “тиканьями” которых
. Наблюдатель X
видит движущиеся часы, время между “тиканьями” которых ![]() ,
тогда при
,
тогда при ![]() и из (6.1) получаем
и из (6.1) получаем ![]() . Таким образом,
. Таким образом, ![]() .
.
Для наблюдателя X часы
движутся со скоростью ![]() ,
он их видит при
,
он их видит при ![]() , подставив в (6.1),
получаем
, подставив в (6.1),
получаем ![]() , тогда
, тогда ![]() .
.
Чтобы найти коэффициент ![]() , поместим часы в начало координатX. В соответствии с принципом относительности
наблюдатель
, поместим часы в начало координатX. В соответствии с принципом относительности
наблюдатель ![]() видит их удаляющимися влево со
скоростью
видит их удаляющимися влево со
скоростью ![]() . Таким образом,
. Таким образом, ![]() при x=0. Тогда из (6.1) получаем
при x=0. Тогда из (6.1) получаем
![]() и
и
![]() . С учетом сказанного уравнения (6.1) пронимают вид:
. С учетом сказанного уравнения (6.1) пронимают вид:
![]()
Известно, что при x=ct
![]() . Подставив это выражение в последнюю
систему уравнений и разделив первое уравнение на второе, получаем:
. Подставив это выражение в последнюю
систему уравнений и разделив первое уравнение на второе, получаем:
![]() .
.
Отсюда 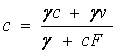 , и
, и ![]() .
.
Мы получили все коэффициенты уравнений (6.1), тогда эти уравнения принимают вид:
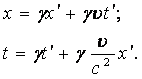 (6.2)
(6.2)
Эта система уравнений в физике называется преобразованиями Лоренца. Она выражает штрихованные координаты через нештрихованные. Обратные преобразования
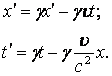
6.3. СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
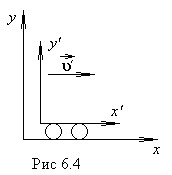 Предположим теперь, что наблюдатель Xрешил измерить длину метровой
линейки, покоящейся относительно штрихованной системы координат, сама же
система координат
Предположим теперь, что наблюдатель Xрешил измерить длину метровой
линейки, покоящейся относительно штрихованной системы координат, сама же
система координат ![]() движется относительно
нештрихованной X со
скоростью
движется относительно
нештрихованной X со
скоростью ![]() (рис.6.4). Концы этой линейки
закреплены в точках
(рис.6.4). Концы этой линейки
закреплены в точках ![]() и
и ![]() ,
тогда из преобразований Лоренца получаем:
,
тогда из преобразований Лоренца получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.