6. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Классическая физика
рассматривает движение тел со скоростями, много меньшими скорости света ![]() . При скоростях, близких к скорости
света законы классической механики не выполняются. Эти процессы и явления
рассматривает релятивистская механика или специальная теория относительности.
. При скоростях, близких к скорости
света законы классической механики не выполняются. Эти процессы и явления
рассматривает релятивистская механика или специальная теория относительности.
Специальная теория относительности была создана А. Эйнштейном в 1905году и представляет собой физическую теорию пространства и времени. Основу этой теории образуют два постулата: принцип относительности Эйнштейна и принцип постоянства скорости света.
6.1.ПОСТОЯНСТВО СКОРОСТИ СВЕТА. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ. СВЯЗЬ ПРОСТРАНСТВА И ВРЕМЕНИ
 Главный парадокс
теории относительности заключается в том, что скорость света в пустоте должна
быть одной и той же для всех наблюдателей. Экспериментально установлено
значение скорости света
Главный парадокс
теории относительности заключается в том, что скорость света в пустоте должна
быть одной и той же для всех наблюдателей. Экспериментально установлено
значение скорости света ![]() м/с. Эйнштейн
объяснил этот “странный” результат “странными “ свойствами пространства и времени.
Он предположил, что с точки зрения движущегося наблюдателя пространство
“сокращается” в направлении движения в
м/с. Эйнштейн
объяснил этот “странный” результат “странными “ свойствами пространства и времени.
Он предположил, что с точки зрения движущегося наблюдателя пространство
“сокращается” в направлении движения в ![]() раз,
а время по измерению того же движущегося наблюдателя во столько же раз
“замедляется”. Иными словами, Эйнштейн “поправил” пространство и время , причем
так, чтобы получить правильный результат
раз,
а время по измерению того же движущегося наблюдателя во столько же раз
“замедляется”. Иными словами, Эйнштейн “поправил” пространство и время , причем
так, чтобы получить правильный результат ![]() для
любого светового импульса и любого наблюдателя , движущегося с постоянной
скоростью (
для
любого светового импульса и любого наблюдателя , движущегося с постоянной
скоростью (![]() и
и ![]() -
координата и время, измеренные движущимся наблюдателем). Таким образом, первый
принцип теории относительности – постоянство скорости света во всех
инерциальных системах отсчета.
-
координата и время, измеренные движущимся наблюдателем). Таким образом, первый
принцип теории относительности – постоянство скорости света во всех
инерциальных системах отсчета.
Второй принцип теории относительности – принцип относительности Эйнштейна - является обобщением принципа относительности Галилея на релятивистский случай: законы физики выполняются одинаково во всех инерциальных системах отсчета. Неизменность вида уравнения при замене в нем координат и времени одной системы отсчета координатами и временем другой системы называется инвариантностью. Поэтому принцип относительности можно сформулировать следующим образом: уравнения, выражающие законы
природы, инвариантны по отношению к преобразованиям координат и времени от одной инерциальной системы отсчета к другой.
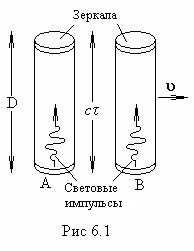
Применим оба принципа
теории относительности к простой разновидности часов – световым часам. Они
представляют собой два обычных зеркала, установленных параллельно друг другу
на расстоянии ![]() (рис.6.1). Такое
устройство может служить своего рода часами, если поверхности зеркал абсолютно
отражающие и короткий световой импульс бегает между ними в прямом и обратном
направлениях. Пусть
(рис.6.1). Такое
устройство может служить своего рода часами, если поверхности зеркал абсолютно
отражающие и короткий световой импульс бегает между ними в прямом и обратном
направлениях. Пусть ![]() - время, за которое импульс
света, отразившись от нижнего зеркала, достигнет верхнего. Часы “тикают” всякий
раз, когда свет отражается от зеркала. Рассмотрим две пары вполне идентичных
часов
- время, за которое импульс
света, отразившись от нижнего зеркала, достигнет верхнего. Часы “тикают” всякий
раз, когда свет отражается от зеркала. Рассмотрим две пары вполне идентичных
часов ![]() и
и ![]() ,
причем частота их синхронизована и период тиканья равен
,
причем частота их синхронизована и период тиканья равен ![]() .
Часы
.
Часы ![]() движутся вправо со скоростью
движутся вправо со скоростью ![]() . Останется ли длина движущихся часов
. Останется ли длина движущихся часов
![]() такой же, как у часов
такой же, как у часов ![]() ? Пусть на конце часов
? Пусть на конце часов ![]() имеется небольшая кисточка с краской.
Когда часы
имеется небольшая кисточка с краской.
Когда часы ![]() проходят мимо часов
проходят мимо часов ![]() , эта кисточка оставляет на часах
, эта кисточка оставляет на часах ![]() метку, и, если метка приходится на
край часов
метку, и, если метка приходится на
край часов ![]() , то это означает, что длина часов
, то это означает, что длина часов ![]() не изменилась. Если же метка
окажется ниже края часов
не изменилась. Если же метка
окажется ниже края часов ![]() , то длина часов
, то длина часов ![]() при движении сократилась.
Предположим, что именно последний случай и реализован в действительности. Тогда
наблюдатель, движущийся вместе с часами
при движении сократилась.
Предположим, что именно последний случай и реализован в действительности. Тогда
наблюдатель, движущийся вместе с часами ![]() ,
увидит, что движущиеся часы
,
увидит, что движущиеся часы ![]() стали короче. С
другой стороны, с точки зрения наблюдателя
стали короче. С
другой стороны, с точки зрения наблюдателя ![]() движущиеся
относительно него световые часы окажутся длиннее. Однако, согласно принципу
относительности, оба наблюдателя совершенно равноправны и оба должны наблюдать
один и тот же эффект. Это возможно лишь в том случае, когда обоим наблюдателям
обе пары часов кажутся одной и той же длины.
движущиеся
относительно него световые часы окажутся длиннее. Однако, согласно принципу
относительности, оба наблюдателя совершенно равноправны и оба должны наблюдать
один и тот же эффект. Это возможно лишь в том случае, когда обоим наблюдателям
обе пары часов кажутся одной и той же длины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.