Специальная теория относительности, страница 7

Однако в выражении (6.5) масса не является постоянной величиной, а зависит от скорости по закону

.        (6.6)

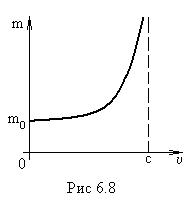
Величина  называется массой покоя, это инвариантная величина, масса  носит название релятивистской массы. Зависимость релятивистской массы от скорости представлена на рис.6.8.

      Продифференцировав выражение (6.5) по времени, получаем релятивистское выражение второго закона Ньютона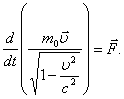  

     Чтобы найти релятивистское выражение для энергии, умножим это уравнение на перемещение частицы :

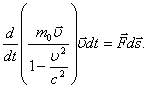
Правая часть этого выражения равна работе, совершаемой над частицей за время dt. Как следует из закона сохранения энергии, эта работа равна приращению энергии частицы:

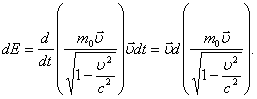
Преобразуем полученное выражение:

Проинтегрировав, имеем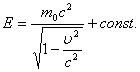  

Экспериментально доказано, что константа в этом выражении равна нулю. Тогда полная энергия частицы

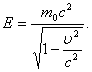                 (6.7)

Если скорость частицы равна нулю,  энергия  Это энергия покоя. Она не связана ни с каким движением частицы. Для произвольного тела энергия покоя равна сумме энергий покоя всех его частиц, кинетических энергий этих частиц в системе центра масс тела и потенциальных энергий взаимодействия этих частиц. В энергию покоя, как и в полную энергию, не входит потенциальная энергия тела в поле внешних сил.

     Очевидно, кинетическая энергия равна разности между полной энергией и энергией покоя частицы:

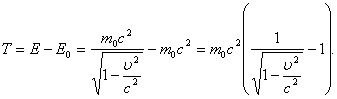
В случае малых скоростей эта формула преобразовывается к виду:

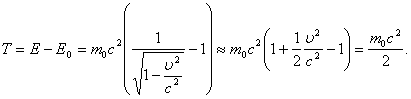
Мы получили классическое выражение для кинетической энергии частицы.

      Решив совместно уравнения (6.5), (6.6) и (6.7), получаем:

.                      (6.8)

При  имеем: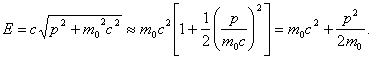

Это выражение отличается от классического выражения  для кинетической энергии слагаемым .

     Из выражения (6.7) следует еще одна формула для энергии: . Тогда импульс частицы

Получим еще одну формулу для энергии. Из замедления времени получаем

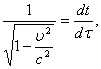
где - промежуток времени между двумя происходящими с частицей событиями, отсчитанный по часам  в той системе отсчета, в которой частица движется, - тот же промежуток времени, отсчитанный по часам, движущимся вместе с частицей. Подставив это выражение в формулу (6.7), имеем

                     (6.9)

     Получим теперь преобразования импульса и энергии. Из (6.8) следует

        (6.10)