Міністерство освіти і науки України
Полтавський державний педагогічний університет ім. В. Г. Короленка
Методи математичної фізики в описі електромагнітного поля
студента фізико-математичного
факультету гр.Ф-51
Геращенка Дмитра Миколайовича
Науковий керівник:
доцент Марченко Валентин Олександрович
Зміст
Вступ……………………………………………………………………………………...2
1.Елементи теорії поля в методах математичної фізики…………………..3
1)характеристики скалярного поля…………………………………………….3
а)градієнт скалярного поля…………………………………………………. 3
б)оператор ![]() (набла)…………………………………………………………4
(набла)…………………………………………………………4
в)лапласіан функції…………………………………………………………...5
2)характеристики векторного поля…………………………………………….6
а)дивергенція і потік………………………………………………………….6
б) теорема Гаусса-Остроградського………………………………………..8
в)ротор векторного поля і циркуляція по заданому контуру……………..11
г)теорема Стокса..............................................................................................13
3)типи векторних полів........................................................................................15
а)потенціальне векторне поле........................................................................15
б)соленоїдальне (трубчасте) векторне поле..................................................15
в)лапласівське (гармонічне) векторне поле..................................................16
4) основна задача векторного аналізу................................................................16
5)диференціальні операції другого порядку.....................................................18
2.Електромагнітне поле через призму теорії поля.....................................19
1)закон збереження електричного заряду.........................................................19
2)закон електромагнітної індукції......................................................................19
3)рівняння магнітостатики..................................................................................20
4)рівняння Максвелла..........................................................................................21
5)електромагнітні хвилі.......................................................................................24
Висновок...........................................................................................................................26
Список використаної літератури....................................................................................27
Вступ
Коло питань, якими займається математична фізика, надзвичайно велике. Сюди можна віднести явища, які вивчаються в гідродинаміці, електродинаміці, теорії пружності, теплопровідності, квантовій механіці, фізиці ядра. Але характерним є те, що при цьому математичні задачі складаються з багатьох загальних елементів, описуються одними математичними законами, які і складають предмет математичної фізики.
Метою написання даної курсової роботи було показати „фізичний зміст” математичних залежностей, що використовуються в описі фізичних полів, зокрема електромагнітного поля.
Електромагнітне поле – це особливий вид матерії, через який здійснюється електромагнітна взаємодія, що є однією з чотирьох типів взаємодій у природі. Внаслідок того, що вона на багато порядків інтенсивніша від гравітаційної та слабкої та є далекодійною, на противагу сильній взаємодії, зустрічається найчастіше і багата проявами в мега-, макро- і мікросвіті.
Різноманітність і багатство проявів електромагнітних явищ потребують їхнього пояснення на основі певних узагальнюючих теоретичних уявлень та математичних закономірностей, які є важливим інструментом пізнання законів природи.
Звісно, обсяг курсової роботи не дозволяє охопити всі можливості матодів математичної фізики при розгляді данного питання, тому в роботі висвітлено основні моменти, що стосуються електромагнітного поля. Зокрема значення введення таких характеристик векторних полів, як ротор і дивергенція, використаня їх в класичній теорії електромагнітного поля, основоположником якої був видатний фізик-теоретик Дж. Максвелл (1831-1879), та класифікації окремих випадків електромагнітного поля.
Відомо, що електромагнітне поле описується системою рівнянь Максвелла,
![]()
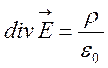 ,
,
![]() ,
,
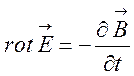 ,
,
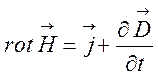 ;
;
які доповнюються рівняннями
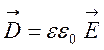 ,
,
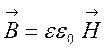 ,
, ![]() ,
,
що була отримана експеримептально і ”вдосконалена” саме завдяки методам математичної фізики.
Так з рівнянь видно нерозривність і матеріальну єдність електричного і магнітного полів, отримано математичний опис та обгрунтування електромагнітних хвиль, знайдено швидкість їх поширення у вакуумі та середовищі тощо.
Елементи теорії поля в методах математичної фізики
Характеристики скалярного поля
Скалярним полем називають частину простору (увесь простір), у кожній точці якого відповідно до певного закону задано числове значення деякої величини.
У загальному випадку скалярне поле характеризують деякою функцією кординат точок простору f(x,y,z) ,яку називають функцією поля. Вважатимемо, що функція поля взагалі однозначна, неперервна і диференційована.
Градієнт скалярного поля
Нехай ![]() та
та ![]() -дві нескінченно близькі точки простору; вектор
-дві нескінченно близькі точки простору; вектор ![]() , що з’єднує ці точки, позначимо через
, що з’єднує ці точки, позначимо через ![]() :
:
![]() .
(1.1)
.
(1.1)
Нехай у просторі задано скалярне поле ![]() . Основну характеристику скалярного
поля – градієнт – введемо, розглядаючи диференціал функції поля:
. Основну характеристику скалярного
поля – градієнт – введемо, розглядаючи диференціал функції поля:
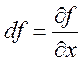
![]() +
+![]()
![]() +
+![]()
![]() .
(1.2)
.
(1.2)
Три величини ![]() ,
,![]() ,
,![]() утворюють,
очевидно, вектор, бо при повороті системи координат OXYZ ці величини –
різниці координат точок
утворюють,
очевидно, вектор, бо при повороті системи координат OXYZ ці величини –
різниці координат точок ![]() та М –
перетворюються за тим же законом, що й координати точки.
та М –
перетворюються за тим же законом, що й координати точки.
(Координати довільної точки М простору
в системах координат ![]() і
і ![]() зв’зані відомим співвідношенням
зв’зані відомим співвідношенням
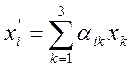 ,
,
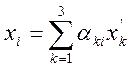 ,(і=1,2,3),
,(і=1,2,3),
де ![]() - координати точки М відносно
системи
- координати точки М відносно
системи ![]() , а
, а ![]() -
відносно
-
відносно ![]() ;
; 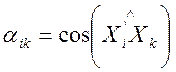 .
Ці формули є відправними для аналітичного означення вектора).
.
Ці формули є відправними для аналітичного означення вектора).
Ліва частина (1.2) не змінюється при повороті
осей OXYZ (інваріантна відносно повороту осей), бо вона є приростом
функції поля при переході від точки М до точки ![]() .
.
Тому з формули (1.2) випливає, що три числа ![]() ,
,![]() ,
,![]() разом утворюють вектор. Цей вектор,
визначений у кожній точці скалярного поля, називають градієнтом поля і
позначають символом gradf:
разом утворюють вектор. Цей вектор,
визначений у кожній точці скалярного поля, називають градієнтом поля і
позначають символом gradf:
gradf=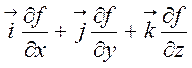 .
(1.3)
.
(1.3)
Формулу (1.2) для диференціала функції поля на підставі (1.3) та (1.1) перепишемо у вигляді:
![]() gradf
gradf![]()
![]() ,
(1.4)
,
(1.4)
тобто як скалярний добуток двох векторів, один
з яких gradf, а
другий – нескінченно мале переміщення ![]() .
.
З (1.3) видно, що абсолютну величину градієнта можна обчислити за формулою:
![]()
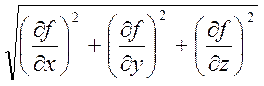 . (1.5)
. (1.5)
Як вектор, градієнт не залежить від орієнтації
осей декартової системи координат. З поворотом осей системи координат OXYZ
змінюються тільки складові градієнта ![]() ,
,![]() ,
,![]() ,
але сам векторgradf не змінюється.
,
але сам векторgradf не змінюється.
Оператор ![]() (набла)
(набла)
Для спрощення обчислень Гамільтон увів для
користування оператор ![]() (читається „набла”) такого
виду:
(читається „набла”) такого
виду:
![]() =
=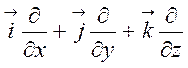 .
(1.6)
.
(1.6)
Властивості цього оператора здебільшого такі
ж, як і властивості вектора. Тому оператор ![]() записують
у вигляді
записують
у вигляді
![]() =
=![]() , (1.7)
, (1.7)
і ![]() ,
,![]() ,
,![]() розглядають
як “складові вектора”
розглядають
як “складові вектора” ![]() , які за означенням дорівнюють
, які за означенням дорівнюють
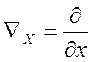 ,
,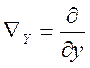 ,
,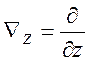 .
(1.8)
.
(1.8)
Тоді градієнт скалярного поля можна розглядати
як добуток символічного вектора ![]() на скаляр f . Справді,
на скаляр f . Справді,
![]()
![]() (
(![]() )f=
)f=![]() . (1.9)
. (1.9)
Але за означенням 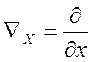 ,
,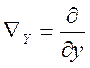 ,
,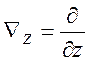 ,
тому
,
тому
![]()
![]()
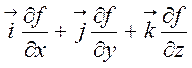 ,
,
або остаточно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.