Цю тотожність широко використовують в теорії електромагнітного поля.
З формули (5.1) видно, що лапсасіан вектора дорівнює
![]() =
=![]() -
-![]() ,
(5.2)
,
(5.2)
тоді як лапсасіан скаляра
![]() =
=![]() . (5.3)
. (5.3)
Електромагнітне поле через призму теорії поля
Закон збереження електричного заряду
Закон збереження електричного заряду можна виразити такою рівністю:
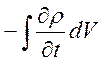 =
=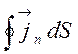 , (6.1)
, (6.1)
де ![]() - об’ємна густина
електричного заряду;
- об’ємна густина
електричного заряду; ![]() - густина струму; вектор
- густина струму; вектор ![]() за напрямом такий самий, як напрям
струму; за абсолютною величиною вектор
за напрямом такий самий, як напрям
струму; за абсолютною величиною вектор ![]() дорівнює
силі струму, що припадає на одиничну площинку, розміщену перпендикулярно до
напрямку руху зарядів.
дорівнює
силі струму, що припадає на одиничну площинку, розміщену перпендикулярно до
напрямку руху зарядів.
За теоремою Гаусса-Остроградського можна записати
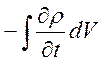 =
=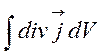 .
(6.2)
.
(6.2)
Оскільки об’єм V в цій рівності цілком довільний, можна ототожнити підінтегральні вирази
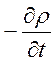 =
=![]() .
(6.3)
.
(6.3)
Отже, використавши теорему Гаусса-Остроградського, отримали закон збереження електричного заряду в диференціальній формі.
Закон електромагнітної індукції
Цей закон є узагальненням відомих
експериментів Фарадея по збудженню струму в замкнутому провідному контурі при
зміні магнітного потоку ![]() , що пронизує
контур:
, що пронизує
контур:
всяка зміна магнітного поля збуджує в
просторі електричне поле, циркуляція напруженості ![]() якого
по довільному замкнутому контуру дорівнює швидкості зміни магнітного потоку
через цей контур.
якого
по довільному замкнутому контуру дорівнює швидкості зміни магнітного потоку
через цей контур.
Закон Фарадея виражають формулою:
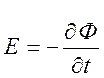 ,
(6.4)
,
(6.4)
де Е – циркуляція вектора електричної
напруженості ![]() по контуру С,
виміряна у вольтах,
по контуру С,
виміряна у вольтах, 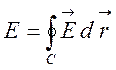 , а Ф – магнітний
потік через контур С, виміряний у веберах, тобто потік вектора магнітної
індукції
, а Ф – магнітний
потік через контур С, виміряний у веберах, тобто потік вектора магнітної
індукції ![]() через поверхню S:
через поверхню S: 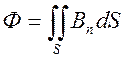 .
.
Підставляючи Ф і Е в (6.4), дістанемо:
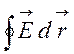 =
=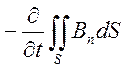 . (6.5)
. (6.5)
Знак мінус означає, що напрям електрорушійної сили індукції (технічний напрям індукційного струму в провідному контурі) утворює з напрямом зростання потоку індукції через контур гвинт з лівою різзю.
За формулою Стокса перетворимо циркуляцію 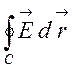 в потік
в потік 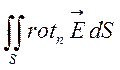 і
перепишемо формулу (6.5) так:
і
перепишемо формулу (6.5) так:
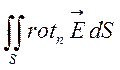 =
=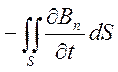 .
(6.6)
.
(6.6)
Ця рівність справедлива для будь-яких поверхонь S ; тому
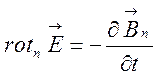 .
(6.7)
.
(6.7)
Напрям проектування ![]() може
бути довідьним, так що з рівності проекцій векторів (на довільний напрям)
випливає також рівність самих векторів:
може
бути довідьним, так що з рівності проекцій векторів (на довільний напрям)
випливає також рівність самих векторів:
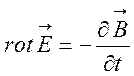 .
(6.8)
.
(6.8)
Це так зване друге рівняння Максвела теорії електромагнітного поля. Рівність (6.8) виконується в кожній точці поля. Друге рівняння Максвела є одним з основних рівнянь теорії електромагнітних процесів.
Рівняння магнітостатики
Нехай в деякому середовищі задано магнітне
поле, утворене постійними магнітами або постійним електричним струмом, ![]() - вектор магнітної напруженості;
- вектор магнітної напруженості; ![]() - густина струму,
- густина струму, ![]() - коефіцієнт магнітної проникності
середовища. Напрям вектора
- коефіцієнт магнітної проникності
середовища. Напрям вектора ![]() визначається
правилом гвинта з правою різзю.
визначається
правилом гвинта з правою різзю.
В якості відправних пунктів при складанні
диференціальних рівнянь, яким повинен задовольняти вектор ![]() , візьмемо дві рівності, які можна
вважати експериментально перевіреними:
, візьмемо дві рівності, які можна
вважати експериментально перевіреними:
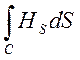 =
=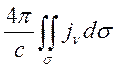 ,
(7.1)
,
(7.1)
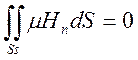 ,
,
де с – електродинамічна стала.
Перше з цих рівнянь є узагальненим законом
Біо-Савара-Лапласа, друге – закон збереження силових ліній вектора ![]()
![]() (опис
в даному і наступному розділах зроблено в системі одиниць СГС), утвореного
векторм
(опис
в даному і наступному розділах зроблено в системі одиниць СГС), утвореного
векторм ![]() та додатковим вектором, що
отримується за рахунок намагнічування середовища. Використавши формули Стокса
та Остроградського–Гаусса, отримаємо так звану систему рівнянь магнітостатики:
та додатковим вектором, що
отримується за рахунок намагнічування середовища. Використавши формули Стокса
та Остроградського–Гаусса, отримаємо так звану систему рівнянь магнітостатики:
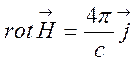 ,
,![]() .
(7.2)
.
(7.2)
У випадку, якщо ![]() =0
магнітне поле буде потенціальним
=0
магнітне поле буде потенціальним ![]() =
=![]() і потенціальна функція u буде
задовольняти рівняння
і потенціальна функція u буде
задовольняти рівняння ![]() , яке у випадку однорідного
середовища співпаде з рівнянням Лапласа:
, яке у випадку однорідного
середовища співпаде з рівнянням Лапласа:
![]() .
(7.3)
.
(7.3)
Можна показати, що поле магнітної індукції, яке описується законом Біо-Савара-Лапласа
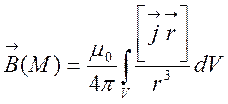 ,
(7.4)
,
(7.4)
є соленоїдальним з векторним потенціалом 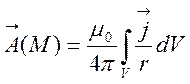 , де
, де ![]() -
магнітна стала.
-
магнітна стала.
Досить переконатись, що ![]() =
=![]() .
Маємо
.
Маємо
![]() =
=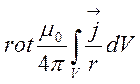 =
=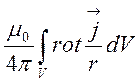 .
.
Але за формулою (2.23)
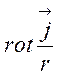 =
=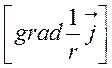 =
=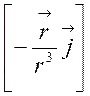 =
=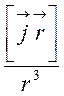 ,
,
(оскільки густина струму ![]() в елементі dV не залежить від координат точки
спостереження, в якій визначаються
в елементі dV не залежить від координат точки
спостереження, в якій визначаються ![]() ,
,![]() , і тому
, і тому ![]() )
тому
)
тому
![]() =
=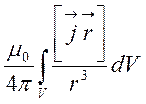 =
=![]() ,
,
що й потрібно було показати.
Рівняння Максвелла
Нехай в деякому середовищі дано змінне
магнітне поле, ![]() - напруженість цього поля,
- напруженість цього поля,
![]() і
і ![]() -
діелектрична і магнітна проникності середовища. В силу експериментально
встановленого закону Фарадея зміна магнітного поля індукує напруженість
електричного поля. Нехай
-
діелектрична і магнітна проникності середовища. В силу експериментально
встановленого закону Фарадея зміна магнітного поля індукує напруженість
електричного поля. Нехай ![]() - напруженість
електричного поля.
- напруженість
електричного поля.
Математично вказаний закон Фарадея можна записати так:
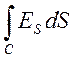 =
=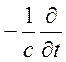
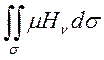 .
(7.5)
.
(7.5)
Використовуючи теорему Стокса, цю рівність можна переписати
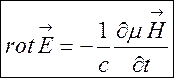 .
(7.6)
.
(7.6)
В якості другого рівняння для визначення ![]() і
і ![]() можна
взяти перше з рівнянь магнітостатики (7.2) у вигляді
можна
взяти перше з рівнянь магнітостатики (7.2) у вигляді
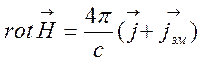 ,
,
де ![]() - струм
провідності, а
- струм
провідності, а ![]() зм –
струм зміщення, який можна визначити як
зм –
струм зміщення, який можна визначити як
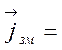
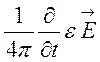 . (див.
1, ст.21)
. (див.
1, ст.21)
Таким чином, отримаємо наступне диференціальне рівняння
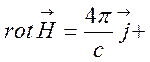
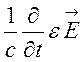 ,
(7.7)
,
(7.7)
де ![]() - струм
провідності, що визначається законом Ома
- струм
провідності, що визначається законом Ома
![]() =
=![]() ,
,
де ![]() - коефіцієнт
провідності середовища.
- коефіцієнт
провідності середовища.
Отримані рівняння доповнюються ще рівняннями
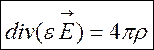 ,
, 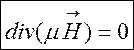 , (7.8)
, (7.8)
які є сумісними з рівняннями (7.6) і (7.7).
Справді, з рівняння (7.6) та з рівняння неперервності
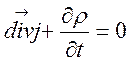
слідує
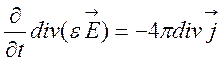 =
=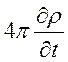 ,
, ![]() .
.
З рівняння (7.7) отримуємо
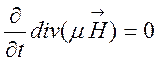 ,
, ![]() .
.
Таким чином, видно, що рівняння (7.8) накладають тільки деякі обмеження на вибір перших двох рівнянь в початковий момент часу.
Розв’язок системи рівнянь електродинаміки
![]()
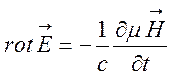 ,
,
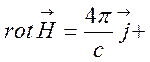
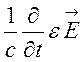 ,
,
![]() ,
,
![]()
 (7.9)
в багатьох загальних випадках можна знайти через допоміжні потенціальні
функції.
(7.9)
в багатьох загальних випадках можна знайти через допоміжні потенціальні
функції.
Нехай, наприклад, середовище є однорідною і
непровідною, тобто ![]() . Тоді четверте рівняння
(7.9) запишеться
. Тоді четверте рівняння
(7.9) запишеться
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.