Методи математичної фізики в описі електромагнітного поля, страница 6

,                                                (7.10)

де  - вектор, визначений з точністю до градієнта довільної функції, а друге із вказаних рівнянь подібно до (7.10) запишеться у вигляді

.

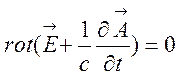звідки

=,                                         (7.11)

де  - деяка функція.

Введені таким чином векторний потенціал  та скалярний потенціал  визначені неоднозначно. Позбавимося цієї неоднозначності, використавши те, що визначеними ними поле векторів  і  було єдиним. Для цього, як видно з рівностей (7.10) і (7.11), достатньо покласти

=, =+,                              (7.12)

де  - якийсь фіксований розв’язок рівняння ,   - якась функція, що задовольняє рівняння , а  - довільна функція. Тепер потрібно вибрати  так, щоб виконувалося так зване співвідношення Лоренца

+=0.                                   (7.13)

Для цього достатньо вимагати, щоб функція  задовольняла рівняння

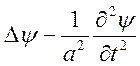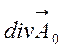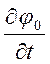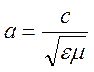=+, ,                (7.14)

тому можна вважати, що співвідношення (7.13) виконується. Тепер в силу (7.10) і (7.11) третє і перше з рівнянь (7.9) можна записати

                                                ,

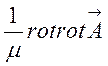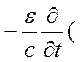
=).                             (7.14)

Ці рівняння в свою чергу, та враховуючи (7.13), якщо врахувати тотожність (5.1) запишуться у вигляді

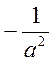
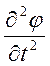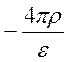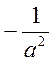
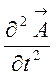=, =0, 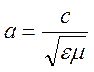.              (7.15)

Таким чином, в розглядуваному випадку, тобто в неоднорідному непровідному середовищі, шість невідомих функцій в системі рівнянь (7.9) виражаються через чотири функції – через векторний потенціал  і скалярний потенціал , які визначаються з системи рівнянь (7.15).

Із загальних рівнянь електродинаміки як частинний випадок отримуються рівняння постійного струму. Тобто, якщо вважати, що вектори  та  не залежать від часу, то з другого і третього рівняння (7.9) отримуємо систему рівнянь постійного електричного струму у вигляді

, .

Електромагнітні хвилі

При перетворення, за якими Максвелл відкрив електромагнітні хвилі, можна показати в дії диференціальні операції другого порядку.

Електромагнітні процеси у вакуумі характеризуються рівняннями Максвела

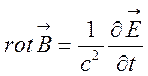,                                                  (8.1)

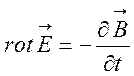,                                                  (8.2)

які справджуються в кожній точці постору, де відсутні струми провідності.

Щоб виключитиз цих рівнянь, наприклад, магнітну індукцію , про диференціюємо перше рівняння () за часом, а на друге подіємо оператором ротор:

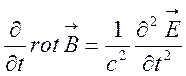,                                             (8.3)

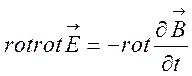.                                             (8.4)

Оскільки 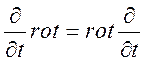, то з порівняння цих рівностей знаходимо

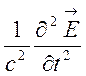.                                              (8.5)

Використавши далі тотожність (5.1) у вигляді

,

і взявши до уваги, що в просторі, де відсутні електричні заряди, , отримаємо для вакууму

,

а рівняння (8.5) остаточно набирає вигляду

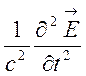.                                                 (8.6)

Аналогічне виключення з рівнянь(8.1) і (8.2) вектора  дає :

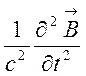.                                                 (8.7)

Так дістають дуже важливі так звані хвильові рівняння (8.6) і (8.7), з яких можна знайти швидкість поширення електромагнітних хвиль. У вакуумі вона рівна с – швидкості світла, а якщо врахувати, що в середовищі

,  ,

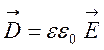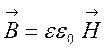то швидкість поширення буде рівна .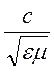

Висновок

Таким чином, узагальнивши експериментальні дані та описавши їх математично, було зроблено виснивок, що електромагнітне поле може існувати вільно, незалежно від джерел, які його створили, у вигляді електромагнітних хвиль. У 1865 році Дж. Максвелл теоретично показав, що електромагнітні коливання за своєю внутрішньою природою мають властивістьть поширюватись зі швидкістю світла. Цей теоретичний висновок було підтверджено у 1888 роцці дослідамми німецького фізика Г. Герца, що відіграло вирішальну роль в утвердженні єдиної природи електричних, магнітних і світлових явищ.

Електромагнітне поле у вакуумі характеризуєтьтся векторами напруженості електричного поля  й індукції магнітного поля . Цими векторами визначаються сили, які діють з боку електромагнітного поля на рухомі і нерухомі електрично заряджені частинки.  У середовищі електромагнітне поле характеризують двома додатковими параметрами : вектором індукції (зміщення) електричного поля  і вектором напруженості магнітного поля .

Електромагнітне поле в будь-якому середовищі описується в макроскопічній електродинаміці системою рівнянь Максвелла, які дають можливість визначити силові характеристики поля  і  залежно від розподілу зарядів і струмів. Вихрове електричне поле збуджується змінним магнітним полем, а вихророве магнітне поле – змінним у часі електричним полем. Якщо в певній частині простору виникає змінне електричне поле, то в сусідніх точках виникає змінне магнітне поле, яке, в свою чергу, зумовлює появу в сусідніх точках змінного електричного поля і т. д. Періодичні зміни електричного і магнітного полів становлять електромагнітне поле як форму матерії, через яку електромагнітна взаємодія між матеріальними електрично зарядженими частинками.

Система рівнянь Максвела описує величезну область фізичних явищ. Ці рівняння лежать в основі розрахунків задач електро- і радіотехніки, теорї і практики магнітної гідродинаміки, нелінійної оптики, вони відіграють велику роль у розвитку фізики  плазми та у вирішенні порблем термоядерного синтезу, їх застосовують при розрахунках присорювачів елементарних частинок, в астрофізиці тощо.

Список використаної літератури

1.           Г. Н. Положий. Уравнения математической физики. – М.: Высшая школа, 1964.

2.  Г. О. Бугаєнко. Методи математичної фізики. – К.: Вища школа, 1970.

3.  А. И. Болсун, В. К. Гронский, А. А. Бейда. Методы математической физики. – Минск: Вышэйшая школа, 1988.

4.  Ю. С. Очан. Методы математической физики. – М.: Высшая школа, 1965.

5.  І. І. Біленко. Фізичний словник. – К.: Вища школа, 1979.

6.  І. М. Кучерук, І. Т. Горбачук, П. П. Луцик. Загальний курс фізики у трьох томах. Том 2. Електрика і магнетизм. – К.: Техніка, 2001.