Методи математичної фізики в описі електромагнітного поля, страница 2

gradf.                                                (1.10)

Складові градієнта позначають так:

,

,

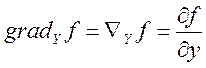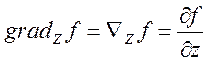.                                          (1.11)

У символічній формі запису формула (1.4) для диференціала функції має вигляд

.

Лапласіан функції

Нехай у просторі існує скалярне поле . Лапсасіаном функції fназивають вираз divgrad f ,який позначають  (читається “лапласіан f“):

= divgrad f.                                              (1.12)

В декартових координатах маємо:

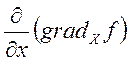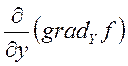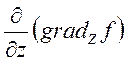=++,                        (1.13)

або

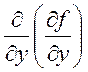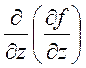=++,                                 (1.14)

остаточно

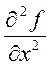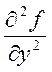=++.                                        (1.15)

Отже, в декартових координатах лапсасіан функції дорівнює сумі її трьох частинних похідних другого порядку по координатах.

Сам оператор Лапласа має вигляд:

=++                                          (1.16)

і його можна розглядати формально як скалярний добуток  :

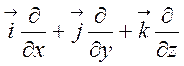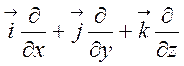=()().                     (1.17)

Формально перемножуючи вирази, матимемо ++,тобто лапсасіан.

Оскільки , а скалярний добуток дорівнює квадрату модуля , то .                                              (1.18)

Отже, лапласіан функції можна позначити як символом  , так і символом  .

Характеристики векторного поля

Векторним полем називають частину простору (увесь простір), у кожній точці відповідно до певного закону  задано деякий  вектор.

З погляду математики задання векторного поля еквівалентне заданню векторної функції , яку ми вважатимемо однозначною, неперервною, диференційованою.

Дивергенція і потік

Розглянемо поле   з складовими по осях:

,,.

Дивергенцією вектора (пишуть ) називають суму частинних похідних виду

=++.                                        (2.1)

Дивергенція однозначно віднесена до кожної точки векторного поля і визначає певне скалярне поле.

Дивергенцію вектора  (тобто векторного поля ) можна розглядати як формальний скалярний добуток “вектора”  на вектор поля  . Справді, обчислення скалярного добутку дає

=()()=(++),           (2.2)

тому що

===1, a ===0.

Якщо врахувати, що 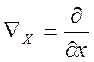, , 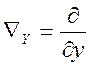 то

=++,                                      (2.3)

і остаточно

=.                                                (2.4)

Хоч доданки формули (2.1) для дивергенції за виглядом і пов’язані з напрямом осей декартової системи координат, та їх сума  не залежить від орієнтації осей, тобто є інваріантом. Формально це можна обґрунтувати так: =, а скалярний добуток двох векторів має інваріантний зміст, незалежний від вибору системи координат.

Властивості дивергенції

Дивергенція є лінійним оператором. Це означає: якщо  і  -векторні поля, для яких існують дивергенції, а  і  -константи, то для поля  теж існує дивергенція, яка дорівнює

+.                                    (2.5)

Властивість лінійності випливає безпосередньо з означення дивергенції.

Взагалі дивергенція існує не для будь-якого векторного поля: складові вектора  мають бути неперервними разом з першими похідними по кожній координаті.

Друга властивість дивергенції виражається формулою

, де                                   (2.6)

u=u(x,y,z)- деяке скалярне поле.

Цю тотожність легко перевірити, користуючись формулою (2.1) для дивергенції в декартових координатах.

Потік

З дивергенцією тісно пов’язане поняття потоку векторного поля.

В заданому векторному полі  візьмемо нескінченно малу площинку dS з одиничним вектором нормалі ( перпендикулярний доdS в певній точці Р площинки). Розглянемо в точці Р вектор поля  і позначимо через а_n його проекцію на нормаль. Добуток а_n і dS, тобто величину

dN= а_ndS(2.7)

називають елементарним потоком вектора поля

  (мал. 1).

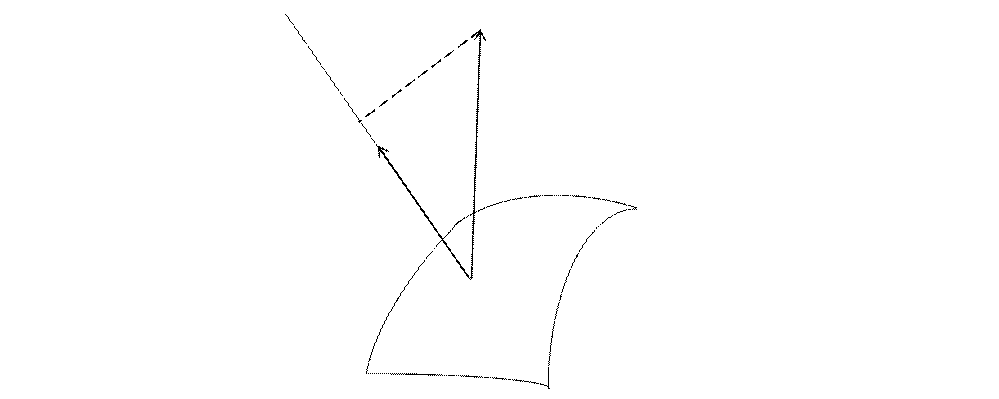мал. 1

Векторне поле (М)  визначає в точках деякої поверхні S деяку скалярну функцію  (-проекція вектора  на напрям нормалі  в точках поверхні S ). Поверхневий інтеграл

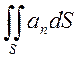
називають потоком вектора  через поверхню S в заданому напрямі . Позначають потік буквою N :

N=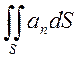,                                                  (2.8)

або

N=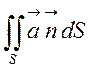,                                                 (2.9)

Отже, потік вектора має зміст поверхневого інтеграла від нормальної складової вектора поля.

Потік N має одну цікаву властивість. Якщо об’єм V ,обмежений поверхнею S, поділити перегородкою  на дві довільні частини V₁ і V₂, обмежені поверхнями S₁+S₁₂ і S₂+S₁₂, то потік через всю зовнішню поверхню S=S₁+S₂ можна розглядати як алгебраїчну суму потоків через поверхні двох об’ємів V₁ і V₂ , на які поділено об’єм V :

N=N₁+N₂.                                                  (2.10)

Для доведення цієї рівності подамо N₁  і N₂ у вигляді

N₁=+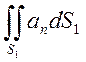

і

N₂=+,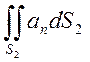

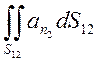де  і  -одиничні нормалі до поверхні (див. мал.2).

мал.2

Оскільки другі доданки правої частини відрізняються тільки знаком (бо ), то у виразі N₁+N₂  згадані доданки знищуються.

Доведене твердження справедливе і у випадку довільної кількості перегородок, тому що об’єми V₁  і V₂ можна також поділити на дві частини, а утворені нові об’єми ще на дві частини і т. д.

Підкреслимо, що інтеграл  називають терміном „потік” незалежно від фізичного змісту вектора .

Теорема Гаусса – Остроградського

Після розгляду дивергенції та потоку встановимо зв’язок між ними. Побудуємо у заданому векторному полі  невеликий паралелепіпед з центром у довільній точці M(x,y,z) (див. мал.3), грані якого нехай паралельні координатним площинам, а ребра дорівнюють ,,. Обчислимо потік вектора поля через поверхню паралелепіпеда.

мал. 3

Позначимо через М₁ і М₂ центри тих граней, які перпендикулярні до осі OY; координати цих точок такі:, .

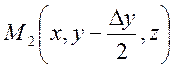Потік вектора  через грань паралелепіпеда з ценром М₁ в напрямі зовнішньої до паралелепіпеда нормалі дорівнює за (2.7)

=,                                            (2.11)

а через грань з центром М₂

==.                            (2.12)

Тут враховано, що напрям зовнішньої до паралелепіпеда нормалі в точці М₂ ( тобто напрям –Y) протилежний напряму OY  і тому проекція вектора  на напрям –Y відрізняється знаком від проекції на напрям Yосі OY.