Методи математичної фізики в описі електромагнітного поля, страница 3

Сума потоків (2.11) та (2.12) через дві протилежні грані паралелепіпеда дорівнює

=+=.                       (2.13)

Але

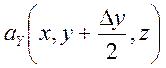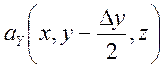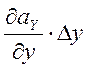-=-=.          (2.14)

Тут  знехтувано доданками, які є малими другого і більш високого порядку, бо можна вважати, що ,,.

На підставі (2.14) формула (2.13) остаточно така:

=.

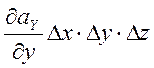За аналогією напишемо ще дві формули для потоків через  інші дві пари граней

=,

=.

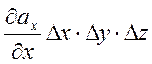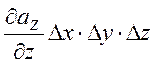Повний потік вектора  через поверхню паралелепіпеда дорівнює

=++=(++,

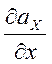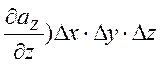або з (2.1)

   (коли ,,),                 (2.15)

де = - об’єм паралелепіпеда.

Візьмемо довільний об’єм V , обмежений замкнутою поверхнею S , роздрібимо його на сукупність елементарних паралелепіпедів трьома сімействами площин, паралельних координатним, і додамо рівності типу (2.15) для всіх елементарних паралелепіпедів об’єму V . на підставі властивості потоку (2.9) в одній частині рівності дістанемо потік вектора  через зовнішню границю S об’єму V , а в другій частині матимемо об’ємний інтеграл від дивергенції

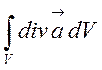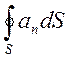=.                                            (2.16)

Ця рівність виражає теорему Гаусса - Остроградського. Дана теорема справджується незалежно від фізичного змісту векторного поля  , яке має бути однозначним, неперервним і диференційованим.

Теорема Гаусса – Остроградського поширюється і на випадок, коли зв’язний об’єм V обмежений не однією, а кількома замкнутими поверхнями S_i:

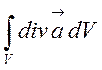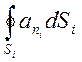=.                                       (2.17)

Напрям нормалей   до всіх поверхонь S_i повинен бути зовнішнім для об’єму V.

Ротор і циркуляція вектора по заданому контуру

За означенням векторний добуток 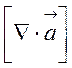 називають ротором вектора і пишуть

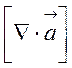=.                                                  (2.18)

Маємо два інваріанти векторного поля: скаляр  (дивергенція) і вектор 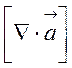 (ротор).

За формулою (2.18)

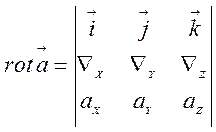,                                             (2.19)

оскільки

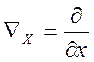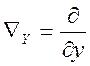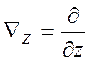, ,,то

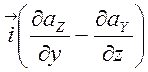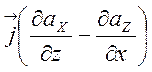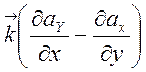=++.                   (2.20)

Ротор однозначно визначений у кожній точці векторного поля.

Складові вектора  позначають так:

==,

==,

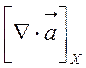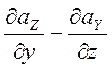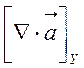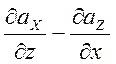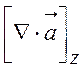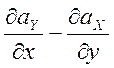==.                               (2.21)

Властивості ротора

Ротор – лінійна дія: якщо  і  -векторні поля, для яких існують ротори, а  і  -константи, то для поля  теж існує ротор, який дорівнює

+.                                   (2.22)

Лінійність операції ротор випливає з означення ротора.

Потрібно відмітити ще тотожність

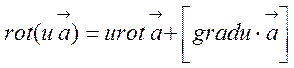,                                     (2.23)

яку легко довести шляхом обчислення складових в декартових координатах. Дійсно, згідно з (2.23) маємо

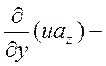
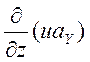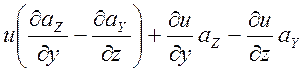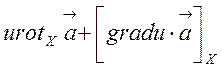===. (2.24)

Аналогічно встановлюємо ще дві формули для складових по осях OY і OZ, після чого переконуємося в справедливості формули (2.23).

Циркуляція вектора по заданому контуру

З ротором пов’язують поняття циркуляції.

В заданому векторному полі (М) візьмемо деяку криву АВ і поділимо її точками М₀=А, М₁, М₂,…,М_п=В на п невеликих частин.

 

мал. 4

Нехай ==.

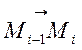Розглянемо суму скалярних добутків

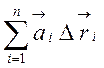,                                                     (2.25)

де - вектор поля , взятий в якій – небудь точці дільниці М_і-1М_і , наприклад в точці  М_і-1 .

Нехай кількість елементів М_і-1М_і  необмежено зростає, тобто , і довжина кожного з них прямує до нуля. Якщо зазгаданих умов існує границя суми (2.25), то цю границю називають криволінійним інтегралом вздовж АВ і позначають

lim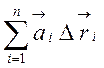=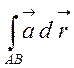.                                          (2.26)

Користуючись формулою скалярного добутку останню рівність можна переписати

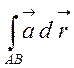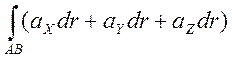=.                                       (2.27)

Криволінійний інтеграл по замкненому контуру називається циркуляцією векторапо замкненому  контуру:

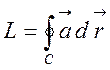,                                                  (2.28)

де С – контур, L – позначення циркуляції.

Теорема Стокса

В полі (x,y,z) розглянемо довільний замкнений контур С , який обмежує площуS і нехай точка М лежить десь в середині контура. Оберемо один з двох можливих напрямів обходу вздовж контура за додатній і побудуємо відповідно до правила  гвинта з правоб різзю вектор нормалі  до площини контура в точці М . Відношення цмркуляції поля до площі

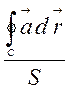,                                              (2.29)

називається середнім завихренням поля (x,y,z) по контуру С.

Перейдеио до границі, вважаючи, що контур С стягується в точку М , залишаючись в одній площині. За такої умови, якщо існує границя середнього завихрення (незалежна від способу стягування коетура С в точку М ) цю границю називають завихренням поля (x,y,z) в точці М навколо напряму . Позначають завихрення через :

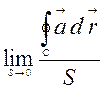=.                                             (2.30)

Можна показати, що вектор завихрення  дорівнює ротору поля

.                                                (2.31)

(Див. Теорему в 2. ст.49-51).

Тоді справедлива рівність

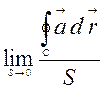=.                                       (2.32)

Розглянемо у просторі, де задано векторне поле , довільну поверхнюS, , яка обмежена контуром C(див мал.5)

                                                                                        

                                                              S     

                                                                                          

                                               С

Мал.5

Поділимо поверхню S двома сімействами кривих на невеликі елементи і кожному елементу поставимо у відповідність нормаль, напрям якої узгоджено з напрямом обходу контура елмента за правилом гвинта з правою різзю. Для кожного елемента поверхні справджуєтьтся рівність (2.32)

=

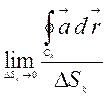
або

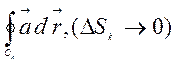=,                                  (2.33)

Додаючи такі рівності до всіх елементів поверхні S , дістанемо в лівій частині інтеграл по поверхні, а в правій – інтеграл по зовнішній межі С .

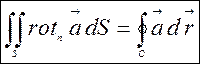.                                       (2.34)

Знайдена формула і виражає другу інтегральну теорему теорії поля – теорему Стокса.

Потік ротора векторного поля  через довільну замкнену поверхню S, обмежену замкнутим контуром С , дорівнює циркуляції вектора  за цим контуром.

Типи векторних полів

Потенціальне векторне поле