Возможные типы кривых свободной поверхности. Построение КСП

4.3.3 Анализ дифференциального уравнения (2)

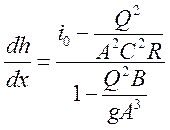
Введем понятие – линия критических глубин (КК). Линия параллельная дну и находящаяся на расстоянии, равном критическом глубине.

Линия нормальных глубин (NN) – это линия параллельная дну и отстоящее от дна на расстояние, равное нормальной глубине .

Установим свойства кривых свободной поверхности (КСП), анализируя уравнение (2).

Как походит КСП к линии нормальных глубин (NN), т.е. при условии, что глубина стремится .

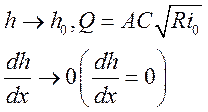 КСП асимптотически стремится к NN.

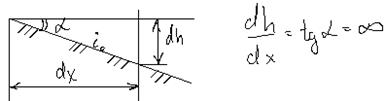
Как подходит КСП к линии КК?

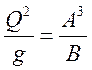 , подставляем зависимость (2), следовательно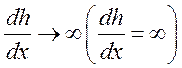

С математической точки зрения – производная это тангенс угла наклона касательной, следовательно, при  КСП подходит к линии КК под прямым углом.

В действительности угол острый.

Что происходит при увеличении глубины ?

Увеличение  ведет к увеличению площади и соответственно . Следовательно 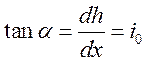, при увеличении глубины КСП стремится к горизонтальной асимптоте.

4.3.4 Возможные типы кривых свободной поверхности

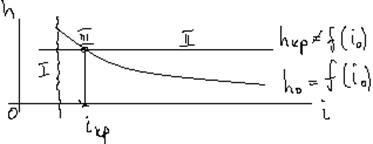
Кривая свободной поверхности в какой-то одной из зон и обозначается соответствующей буквой с индексом.

В зависимости от увеличения или уменьшения глубины КСП, то возможны кривые спада (уменьшение ) или подпора (увеличение по направлению движения).

Случай		промежуточный
Соотношение  и
Соотношение  и
Взаимное положение NN и КК, зоны их маркировка, типы КСП

Кривая свободной поверхности в какой-то одной из зон и обозначается соответствующей буквой с индексом.

В зависимости от увеличения или уменьшения глубины КСП, то возможны кривые спада (уменьшение ) или подпора (увеличение по направлению движения).

Изображаем КСП для случая  и .

Случай  , , зоны нет,  и . Из зависимости (2) получаем 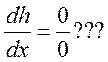. Линии нормальных и критических прямых совмещены, условие подхода каждой между собой несовместимы, следовательно, могут не выполняться, т.е. и не асимптотически будет подходить кривая и не под прямым углом.

Рассматриваем случай , как промежуточный между  и . Сопоставляем для кривой  случаи первый и второй, полагаем, что при переходе от  ко  кривая свободной поверхности проходит через горизонтальное положение. Тоже кривая вида .

Всего 8 типов КСП. В зоне  всегда подпор. В зоне  всегда спад. В зоне  всегда подпор.

К линии нормальных глубин КСП всегда подходит асимптотически.

К линии критических глубин КСП всегда подходит под прямым углом (на самом деле под острым).

Случай третий – особый.

4.3.5 Построение КСП

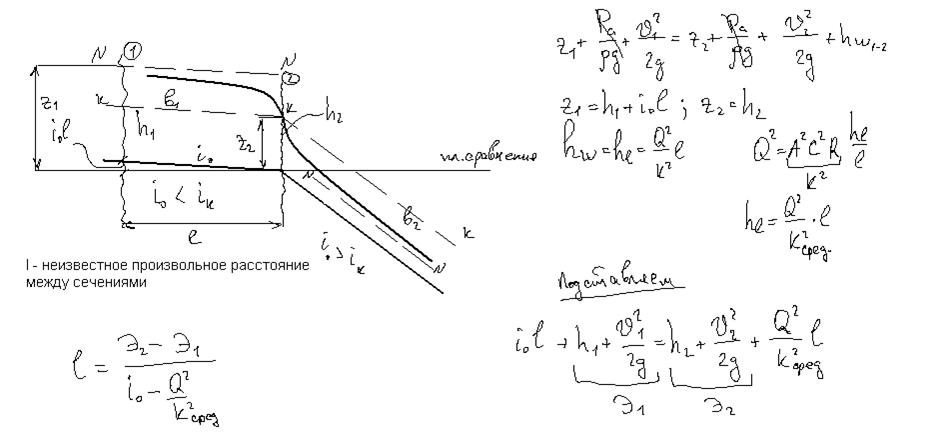
Рассмотрим метод непосредственного применения уравнения Бернулли (метод Чарномского 1914г.), который выгодно отличается простотой и возможностью использования и для не призматических русел.

Изобразим начальный или входной участок быстротока.