Экономика и менеджмент \ Статистика

Сущность статистического наблюдения. Статистическая сводка. Абсолютные и относительные величины: сущность, виды, порядок расчета. Структурные средние величины. Асимметрия и эксцесс, страница 7

Для индексов физического объема в качестве веса соизмерителя может выступать средняя цена на одноименную продукцию 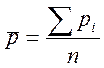, где  - цена продукции в каждом регионе,  - количество произведенной продукции в каждом регионе.

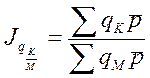
23. Индексы Ласпейреса, Пааше, Лоу.

Индекс цен Ласпейреса – в качестве веса соизмерителя используется физические объемы в базисном периоде. Индекс Ласпейреса показывает, во сколько раз товары базисного периода подорожали за счет изменения цен в текущем периоде, при изменения объема потребительской корзины в текущем периоде. Индекс Ласпейреса и Пааше используются для определения темпов инфляции. На Западе и на Американском континенте для определения индекса инфляции используют индекс Ласпейреса. У нас с началом 90-х годов используют индекс   Ласпейреса вместо Пааше..

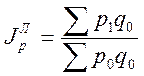  - Ласпейреса

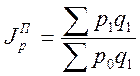 -Пааше.

Индекс Лоу учитывает изменение в ассортиментной политике.

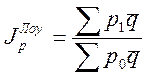, где .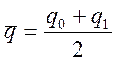

Идеальный индекс Фишера – экономическое содержание даны индекс не имеет, чаще всего он используется для исчисления индексов цен за длительный промежуток времени, так как за это время сглаживается тенденция в составе и структуре цены.

 .

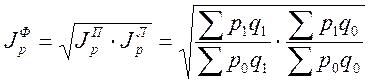24. Понятие корреляции и регрессии. Основные задачи применения корреляционно-регрессионного анализа. Корреляционная таблица. Парная регрессия. Измерение тесноты связи при помощи линейного коэффициента корреляции.

Данный анализ используется для изучения взаимосвязи между результативным и факторным признаком.

Корреляция – определяет количественную зависимость между факторным и результативным признаком.

Регрессия – определение функциональной зависимости между результативным и факторным признаком (определят уравнение регрессии характеризующий вид связи).

Рассчитывается коэффициент корреляции: по шкале Чеддока определяется теснота связей между факторным и результативным признаком.

·  если коэффициент корреляции - связь слабая;

·  если от  до  - средняя;

·  если от  до - высокая, тесная.

Парная регрессия.

При парной регрессии изучается связь между результативным и одним факторным признаком. Связь между этим может быть:

- линейная

- гиперболическая

- параболическая.

Определить тип уравнения можно исследуя зависимость графически. Однако существует более общие принципы:

  1. если результативный и факторный признак возрос одинаково, примерно в арифметической прогрессии, то связь между ними линейная, при обратной связи, связь гиперболическая;
  2. если факторный признак увеличился в арифметической прогрессии, а результативный увеличился значительно быстрее, то используется параболическая или степенная регрессия.

Рассмотрим линейную регрессию.

 - параметры данного уравнения находятся по методу наименьших квадратов ,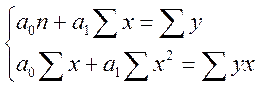

- представляет собой усредненное влияние на результативный признак неучтенных факторов;

- коэффициент регрессии, который показывает, насколько изменится в среднем результативный признак при увеличении факторного на единицу собственного измерения.

Корреляционная таблица.

На практике часто исследуются совокупности, в которых и x и y представлены в виде интервальных рядов. В этом случае в отличии от предыдущего вида значений.

 y                   x

0-2

2-4

4-6

Итого по y

10-12

1

12-14

8

10

14-16

12

Итого по x

Если в корреляционной таблице частоты которые расположены по диагонали, тол связь между  x и y будет прямая     , если - связь обратная. Если частоты расположены вокруг диагонали, то это говорит о наличии связи. Если клетки таблицы заполнены большими числами то связь слабая. Если между значениями в таблице большие промежутки, значения разбросаны хаотично, то связь отсутствует.

Линейный коэффициент корреляции.

Данный коэффициент  - позволяет определить количественную связь между результативным и факторным признаком.

1. , , .

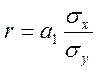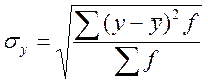2. .

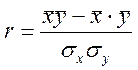3. .

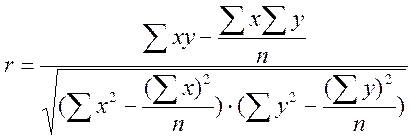25. Парная регрессия для сгруппированных данных. Коэффициент эластичности.

При множественной регрессии на результативный признак влияет несколько факторов. Построение уравнения регрессии состоит из нескольких этапов:

1.  выбор формы связи (которое описывается уравнением регрессии). Наиболее приемлемый способ выбора связи, заключается в переборе различных уравнений. Сущность этого метода заключается в том, что при помощи средств вычислительной техники, с помощью специальных программ рассчитывается уравнение регрессии с последующей статистической проверкой на соответствие критерия Стьюдента  и Фишера, которые являются табличными. Этот метод очень трудоемкий и в основе все модели стараются свести к линейным.

2.   отбор факторных признаков. Сложность их отбора заключается в том, что практически все они связанны между собой. На данном этапе возникает проблема оптимального выбора факторных признаков.

Для выбора факторных признаков используют следующие методы:

- метод экспортных оценок – основан на ранговой зависимости;

- шаговая регрессия – сущность в том, что последовательно в уравнении регрессии включается по одному факторному признаку и рассчитываются критерии, определяющие их значимость.

Коэффициент эластичности. 

Для расчета влияния факторного признака на результативный применяется коэффициент эластичности. Он рассчитывается как для каждой точки совокупности, так и для всей совокупности в целом. Коэффициент эластичности показывает, насколько процентов изменится результативный признак при изменении факторного признака на 1 %.

     .

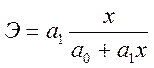26. Коэффициенты корреляции рангов Спирмена, Кэндела, Фехнера.

Существует несколько метод определения тесноты корреляционных связей как для количественных, так и для качественных показателей.

При помощи коэффициента корреляции, основанный на ранжировании:

Скачать файл