2. единицы измерения указываются в отдельных графах или над таблицей;
3. повторяющиеся термины выносятся в общий заголовок;
4. графы и строки необходимо нумеровать;
5. в групповых таблицах всегда должны стоять итоговые графы и строки;
6. округление чисел проводится с одинаковой точностью;
7. в таблицах значимость абсолютных цифр должна быть наименьшей (1253622 = 1,25 млн. руб);
8. делаются сноски, если на ряду с отчетными данными приводятся расчетные;
9. отдельные клетки таблицы могут быть не заполнены по сл. причинам:
· x – клетка не подлежит заполнению
· … - данные отсутствуют
· - - отсутствует изучаемое явление
· 0,0 – при округлении с большей значимостью числа может появиться значимое число 0,001.
Статистические графики.
Для наглядного представления экономических показателей на графиках используют правило золотого сечения.
К обобщающим показателям относятся показатели, которые изучают количественную сторону изучаемых явлений. Обобщающие показатели отражают объемы, уровни (производительность труда, заработная плата) и соотношение (рабочих с высшим и низшим образованием).
Статистические показатели (обобщающие) имеют качественную и количественную характеристику.
Различают:
1. Абсолютные показатели – это именованные числа, имеющие определенную размерность и единицы измерения:
2. Относительные величины – представляют собой соотношение сравниваемых абсолютных величин (в %, в промилях, в долях, в децимилях). Кроме того к относительным величинам относятся такие показатели как урожайность (центнер с га). Различаются следующие виды относительных величин:
Относительная величина выполнения
плана 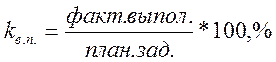
Относительный показатель динамики:
- цепные – если сравниваются смежные уровни ряда динамики – темпы роста.
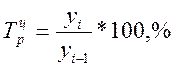 ,
где
,
где ![]() - уровень ряда динамики
- уровень ряда динамики
![]() - предыдущий уровень ряда динамики.
- предыдущий уровень ряда динамики.
- базисные – сравнение происходит с первым уровнем ряда динамики, который принят за базис.
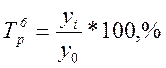 ,
где
,
где ![]() - базовый уровень.
- базовый уровень.
Относительные показатели структуры – они показывают долю изучаемого признака в общем объеме.
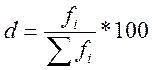
· Относительные показатели интенсивности – характеризуют степень насыщенности данного явления в определенной среде – коэффициент рождаемости/смертности.
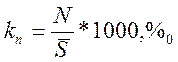 , где
, где ![]() -
коэффициент рождаемости/смертности
-
коэффициент рождаемости/смертности
![]() - число родившихся/умерших
- число родившихся/умерших
![]() - среднегодовая численность
населения.
- среднегодовая численность
населения.
· Показатели координации – характеризуют отношение частей изучаемой совокупности к одной из них, принятой за базу. Данный показатель показывает во сколько раз одна часть совокупности больше другой.
· Показатели сравнения.
Относительные показатели сравнения – они показывают соотношение одноименных абсолютных величин, соответствующих одному и тому же периоду времени, но относящиеся к разным территориальным объектам.
Статистические показатели должны отвечать следующим требованиям:
1. должны выражать сущность изучаемых величин;
2. должны быть сопоставимы;
3. необходимо, чтобы данные показатели охватывали как можно больше изучаемых величин.
5. Степенные средние величины.
Средняя величина – вариант x, который обладает наиболее типическими свойствами изучаемой совокупности.
Типовая формула для расчета
средней величины:![]()
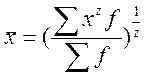
Следующие виды средних величин:
Ср. арифметическая:
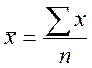 ,
, 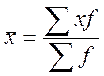 .
.Расчет ср. арифметической зависит от вида ряда, в интервальном необходимо найти середину интервала.
Свойства ср. арифметической:
1. средняя из постоянного числа равна постоянному числу.
2. если все частоты увеличить на одно и то же число или уменьшить, то средняя величина от этого не изменится.
3. если варианты x увеличить или уменьшить на постоянное число, то средняя увеличится или уменьшится на это число.
4. если вариант x увеличить или уменьшить в к раз, то средняя величина изменится в к раз.
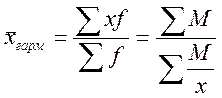 -
применяется наиболее часто для расчета средних цен.
-
применяется наиболее часто для расчета средних цен.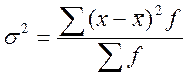 ,
где
,
где 6. Структурные средние величины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.