· на основе одногодичных данных
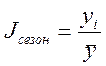 , где
, где ![]() -
значение изучаемого уровня,
-
значение изучаемого уровня, 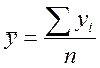
· на основе данных за 3 года
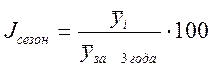 .
.
19. Понятие экономических индексов. Классификация индексов. Индивидуальные и общие индексы. Средние индексы (среднеарифметическая и гармоническая форма общих индексов).
Под индексом понимается относительная величина, количественно характеризующая динамику совокупности, состоящей из непосредственно несоединимых единиц.
Виды индексов.
1. Индивидуальные
индексы ![]() -
рассчитываются для отдельных видов продукции, работ и услуг. Различают
индивидуальные индексы:
-
рассчитываются для отдельных видов продукции, работ и услуг. Различают
индивидуальные индексы:
· качественных
показателей (цена ![]() , себестоимость
, себестоимость ![]() , трудоемкость
, трудоемкость ![]() , выработка продукции
, выработка продукции ![]() ).
).
Индивидуальный
индекс цены: 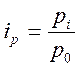 , где
, где ![]() - цена текущего периода,
- цена текущего периода, ![]() - цена базисного периода.
- цена базисного периода.
Индивидуальный
индекс себестоимости: 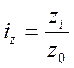 .
.
· Количественных
показателей (количество произведенной продукции ![]() ,
численность
,
численность ![]() )
)
Индивидуальный
индекс физического объема: 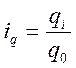 ,
где
,
где ![]() - количество произведенной продукции
в текущем периоде,
- количество произведенной продукции
в текущем периоде, ![]() - количество произведенной
продукции в базисном периоде.
- количество произведенной
продукции в базисном периоде.
На основе
индивидуальных индексов могут быть построены сводные индексы третьего
показателя: ![]() - индивидуальный индекс выручки
(стоимости)
- индивидуальный индекс выручки
(стоимости)
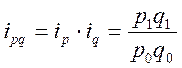 .
.
На основе индексов можно рассчитать абсолютное изменение показателей
Для
индивидуальных индексов цены: ![]()
физический
объем выручки: ![]()
![]() .
.
2. Общие
индексы ![]() - агрегатные, рассчитываются, когда
на одном предприятии производится или продается разнородная продукция. В основе
- агрегатные, рассчитываются, когда
на одном предприятии производится или продается разнородная продукция. В основе
![]() лежат
лежат ![]() .
.
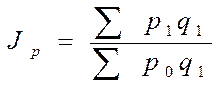 .
.
·
В общих индексах качественных показателей в качестве веса –
соизмерителя выступает количественный показатель (![]() или
или
![]() ) текущего периода. На основе данной
формулы можно определить абсолютное изменение выручки в результате изменения
цен на продукцию
) текущего периода. На основе данной
формулы можно определить абсолютное изменение выручки в результате изменения
цен на продукцию ![]() .
.
Построение общего индекса для количественных показателей:
общий вид
физического объема 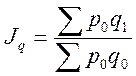 .
.
В качестве
веса соизмерителя для количественных показателей выступает качественный
показатель на базисном уровне. На основе данной формулы можно определить
абсолютное изменение выручки под влиянием проданной или произведенной продукции
![]() .
.
Рассмотрим
взаимосвязь индексов качественного и количественного показателя: ![]() - общий индекс выручки или стоимости
или
- общий индекс выручки или стоимости
или 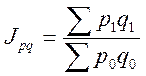 . На основе приведенной формулы можно
рассчитать абсолютное изменение выручки под действием 2-х факторов: цены и
количества
. На основе приведенной формулы можно
рассчитать абсолютное изменение выручки под действием 2-х факторов: цены и
количества ![]() .
.
3. Средние индексы – являются разновидностью общих индексов и применяются в тех случаях, когда неизвестны данные либо за базис, либо за текущий период, но известны индивидуальные индексы изучаемых величин:
· Средне арифметическая
- для количественного
показателя физического объема 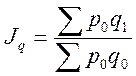 .
.
Под средним
индексом понимается индекс, вычисленный как средняя величина из индивидуальных
индексов 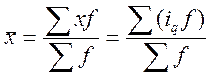 ,
, 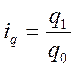 в
качестве
в
качестве ![]() ,
, ![]()
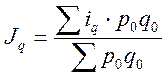
·
Средне гармоническая форма качественных показателей – индекс цены
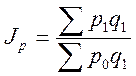 ,
, 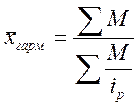 ,
,
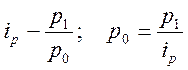
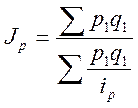 .
.
20. Индексы цепные и базисные, с постоянной и переменной базой сравнения.
Индексы могут быть использованы для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае различаются базисные и цепные индексы.
Базисные индексы используются для наглядной характеристики общей тенденции развития исследуемого явления. Цепные индексы – последовательного изменения уровней в объеме.
Между цепными и базисными индексами существует взаимосвязь:
1. если
известны цепные индексы ![]() ,
,
![]() ,
, ![]() - перемножить эти индексы
- перемножить эти индексы 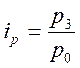
2. если
известны базисные индексы ![]() ,
,
![]() ,
, ![]() - разделить их один на другой
- разделить их один на другой
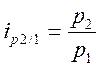 ,
, 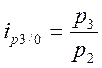 .
.
Аналогично рассчитываются индексы общие.
При построении системы индексов можно использовать индексы с постоянными и переменными весами
Системы индексов с постоянными весами называется системой общих индексов одного и того же явления (р или q), вычисленная с весами, не меняющимися при переходе от одного индекса к другому.
Постоянные веса позволяют исключить влияние изменения структуры на величину индекса.
Например для
индекса физического объема ![]()
- построим систему
базисных индексов с постоянными весами: 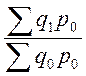
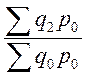
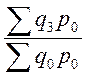 ;
;
- построим
систему цепных индексов с постоянными весами: 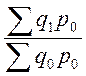
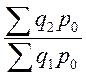
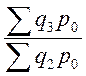 .
.
Система индексов с переменными весами - это система общих индексов одного и того же явления, вычисленных с весами, которые меняются от одного индекса к другому. Переменные веса - веса отчетного периода.
- сис-ма
цепных индексов с перем. весами: 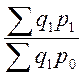
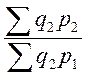
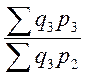 ;
;
- сис-ма
базисных индексов с переем. весами: 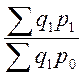
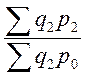
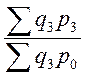 .
.
21. Индексы средних величин (индексы переменного, постоянного состава и структурных сдвигов).
Индексы средние применяются, когда на разных предприятиях производится или продается одна и та же продукция. Для того чтобы сравнить объемы продаж необходимо сравнить средние цены на данный вид продукции. Анализ полученных показателей производят при помощи ср. индексов.
1.
Индекс переменного состава ![]() -
изменение средней цены на продукцию под влиянием 2-х факторов в текущем и в
базисном периоде в среднем по всем предприятиям.
-
изменение средней цены на продукцию под влиянием 2-х факторов в текущем и в
базисном периоде в среднем по всем предприятиям. 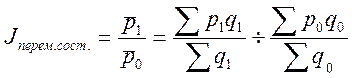 ;
;
![]() .
.
2.
Индекс постоянного состава ![]() Он
показывает на сколько изменится средняя цена на продукцию за счет изменения
цены на каждом предприятии.
Он
показывает на сколько изменится средняя цена на продукцию за счет изменения
цены на каждом предприятии. 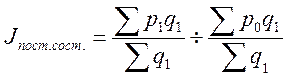 ;
; 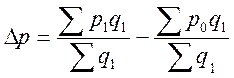 .
.
3.
Индекс структурных сдвигов ![]() В
этом случае изменение средней цены происходит за счет изменения объема продаж
продукции на каждом предприятии.
В
этом случае изменение средней цены происходит за счет изменения объема продаж
продукции на каждом предприятии. 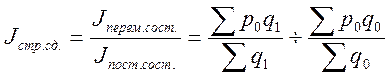 ;
; 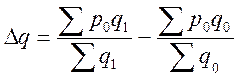 .
.
Взаимосвязь индексов
![]() или
или ![]()
22. Территориальные индексы.
Особенность данных индексов является то, то при двух стороннем сравнении каждый регион может быть принят в качестве сравниваемого, так и в качестве базы сравнения.
При определении общих индексов будет меняться база сравнения. Например:
- для индекса физического объема.
Если сравнивают города К и М, то в качестве базы сравненя будет выступать цена
в городе К ![]() , затем
, затем ![]() .
.
- для индекса цены. В качестве
базы сравнения ![]() ,
, ![]() .
.
Рассмотрим территориальные индексы, если в качестве базы сравнения будет выбран город К.
- база сравнения г. К 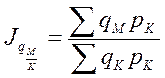
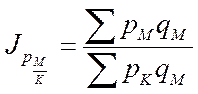 ;
;
- база сравнения г. М 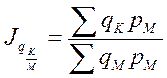
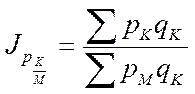 .
.
Если известны
данные на одноименный вид товара в 2-х городах, то общий индекс цены может быть
рассчитан следующим образом: ![]() ,
, 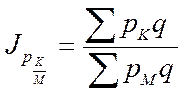 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.