1. Мода (![]() ) – под ней понимается наиболее
часто встречающийся вариант. Мод может быть несколько. Расчет моды зависит от
того, в каком ряду она рассчитывается (в дискретном или в интервалом).
) – под ней понимается наиболее
часто встречающийся вариант. Мод может быть несколько. Расчет моды зависит от
того, в каком ряду она рассчитывается (в дискретном или в интервалом).
а) В
дискретном ряду (ищем ![]() , находим по нему
интервал и строим полигон).
, находим по нему
интервал и строим полигон).
б) В интервальном ряду
ü
Находим ![]()
ü
Находим по ![]() модальный
интервал
модальный
интервал
ü
Находим ![]() по формуле:
по формуле: 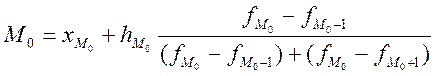 , где
, где ![]() -
начало модального интервала
-
начало модального интервала
![]() - величина модального интервала
- величина модального интервала
![]() - частота модального интервала
- частота модального интервала
![]() - частота до модального интервала
- частота до модального интервала
![]() - частота после модального интервала
- частота после модального интервала
2. Медиана (![]() )- вариант, делящий ранжированный ряд
по полам. Для того, что бы найти медиану, находят ее порядковый номер:
)- вариант, делящий ранжированный ряд
по полам. Для того, что бы найти медиану, находят ее порядковый номер:
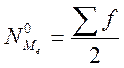 -
для четного количества.
-
для четного количества.
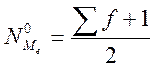 -
для нечетного количества.
-
для нечетного количества.
Затем находят ряд накопленных частот. Расчет медианы зависит от того, в каком ряду она рассчитывается.
а) Для
дискретного ряда: - находим ![]()
- находим накопленную частоту ![]()
- по ![]() и
и ![]() находим
находим
![]() .
.
б) Для интервального ряда. В интервальном ряду медиану рассчитывают по формуле:
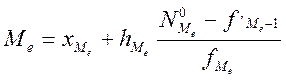 ,
где
,
где
![]() - начало медианного интервала;
- начало медианного интервала;
![]() - величина медианного интервала;
- величина медианного интервала;
![]() - частота медианного интервала;
- частота медианного интервала;
![]() - частота накопленная до медианного
интервала;
- частота накопленная до медианного
интервала;
В
интервальном ряду ![]() можно рассчитывать
графически, построив кумуляту по накопленной частоте.
можно рассчитывать
графически, построив кумуляту по накопленной частоте.
7. Асимметрия и эксцесс.
Расчет данных показателей используется для характеристики кривых распределения, их вытянутость вдоль оси абсцисс- показатели асимметрии, или оси ординат- показатели эксцессов.
Асимметрия – для оценки степени асимметричности применяетсямоментный и структурный коэффициенты асимметрии. В симметричных рядах средние величины равняются моде и равняются медиане. Однако в большинстве своем ряды распределения не симметричны и определяются при помощи показателей асимметрии:
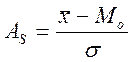
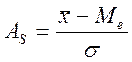
Моментный
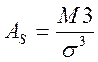 , где
, где ![]() -
центральный момент 3 порядка.
-
центральный момент 3 порядка.
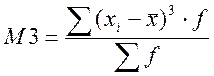 .
.
На направление асимметрии будет указывать знак коэффициента:
![]() - левосторонняя
- левосторонняя
![]() - правосторонняя.
- правосторонняя.
Под эксцессом понимают островершиность или плосковершинность распределения по сравнению с нормальным распределением при той же силе вариации. Определяется только для симметричных или умеренно асимметричных вариаций.
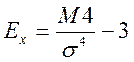
![]() - плосковершинные
- плосковершинные
![]() - островершинные.
- островершинные.
Для определения остро или низко вершинности кривой распределения используются показатели эксцесса, которые рассчитываются по формуле:
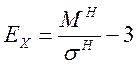
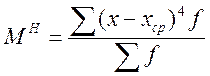
Квартили – значения вариантов, делящих совокупность на 4 равные части.
Децили – значения вариантов, делящих совокупность на 10 равных частей.
При этом различают верхние и нижние квартили и децили. Формулы для расчета квартилей и децилий похожи на формулу для расчета медианы:
Квартили:
Нижний: 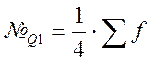
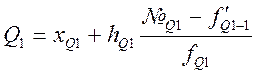
Верхний: 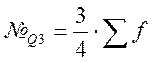
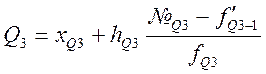
Децили:
Нижний: 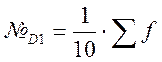
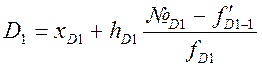
Верхний: 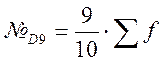
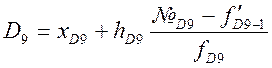
8. Теоретические кривые распределения. Кривая нормального распределения и ее построение по эмпирическим данным.
Графическое представление рядов распределения дает представление о форме распределения (полигон, гистограмма). Однако судить о форме распределения по представленным рядам рискованно, т.к. в них может содержаться недостаточное количество единиц для обследования. При увеличении объема изучаемой совокупности полигон или гистограмма сглаживаются и распределение представляет плавную линию – кривую распределения.
Фактическая кривая отличается от теоретической (плавной кривой) и в статистике выдвигаются и проверяются гипотезы о случайности этих расхождений. Среди кривых распределения особое место занимает кривая нормального распределения, которая имеет колоколообразную форму. Кривая нормального распределения имеет 2 точки перегиба, которые находятся на расстоянии средне квадратического отклонения.
В промежуток:
от ![]() до
до ![]() попадают
68,3 %
попадают
68,3 %
от ![]() до
до ![]() попадают
95,4 %
попадают
95,4 %
от ![]() до
до ![]() попадают
99,7 %.
попадают
99,7 %.
Кривая нормального распределения описывается следующим уравнением:
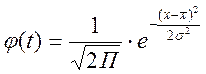
выражение 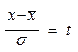 - нормированное отклонение.
- нормированное отклонение.
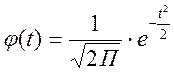 .
.
Кривая
нормального распределения – ордината, является теоретической частотой
![]() . Фактическая частота
(эмпирическая) –
. Фактическая частота
(эмпирическая) – ![]() .
.
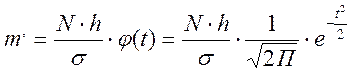 , где
, где ![]() -
количество элементов в изучаемой совокупности,
-
количество элементов в изучаемой совокупности, ![]() -
расстояние между соседними группами.
-
расстояние между соседними группами.
Кроме нормального распределения, на практике встречается и распределение Пуассона. Оно присуще дискретным рядам и возникает в тех случаях, когда сами варианты x являются своего рода частотами в ситуациях, которые встречаются крайне редко. В распределениях Пуассона с увеличением значения x вероятность их наступления падает.
Распределения Пуассона выражается следующей зависимостью для расчета теоретической частоты.
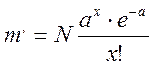
![]() .
.
Распределение Пуассона характерно для редко встречающихся явлений, иногда его называют законом малых чисел.
9. Критерий согласия Пирсона «хи-квадрат». Критерии согласия Романовского, Ястремского, Колмогорова.
Вычисление теоретических частот происходит из предположения, что эмпирическое распределение близко к теоретическому, а расхождения случайны. Случайность отклонений проверяется при помощи критериев согласия:
1. Критерий
![]() - установил Пирсон для оценки
случайности расхождений теоретической и эмпирической частоты. Он разработал
специальные таблицы для расчета
- установил Пирсон для оценки
случайности расхождений теоретической и эмпирической частоты. Он разработал
специальные таблицы для расчета ![]() .
. ![]() - в этом случае отклонения случайны и
эмпирическое распределение будет являться теоретическим.
- в этом случае отклонения случайны и
эмпирическое распределение будет являться теоретическим. 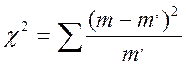 .
.
2. Критерий
Романовского – этот критерий не требует специальных таблиц для определения
существенности расхождений между ![]() и
и ![]() .
. 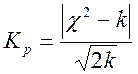 ,
где
,
где ![]() - число степеней свободы.
- число степеней свободы.
![]() - для нормального распределения
- для нормального распределения
![]() - для распределения Пуассона
- для распределения Пуассона
![]() - количество групп в изучаемой
совокупности.
- количество групп в изучаемой
совокупности.
Если ![]() , то расхождение является
несущественным, а распределения можно считать нормальным.
, то расхождение является
несущественным, а распределения можно считать нормальным.
3. Критерий
Ястремского также базируется на основе ![]() ,
но не зависит от числа степеней свободы, а зависит только от количества групп.
,
но не зависит от числа степеней свободы, а зависит только от количества групп.
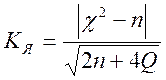 , где
, где ![]() зависит
от количества групп.
зависит
от количества групп.
Гипотеза о
нормальном распределении будет считаться не опровергнутой если ![]() .
.
4. Критерий Колмогорова основан на сопоставлении накопленных частот.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.