Сущность статистического наблюдения. Статистическая сводка. Абсолютные и относительные величины: сущность, виды, порядок расчета. Структурные средние величины. Асимметрия и эксцесс, страница 5

- предельная ошибка в выборке для доли.

Искомые границы будут определяться по формуле:

- для средней величины  или ;

- для доли  или .

Расчет предельной ошибки в выборке зависит от вида выборки и способа отбора.

Предельная ошибка в выборке, рассчитывается двумя способами:

·  Повторный

- для средней величины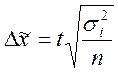

- для доли единиц, обладающих данным признаком 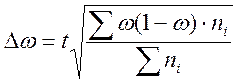, где - численность каждой группы.

·  Бесповторный

- для средней величины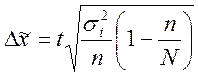

- для доли единиц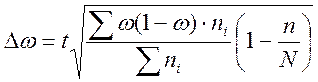

14. Использование формул предельной ошибки выборки. Определение численности выборочной совокупности для собственно-случайной, механической, типической и серийной выборки.

Использование формул предельной ошибки в выборке.

Зная формулы  и  можно решать следующие задачи:

1.  определение доверительных пределов для средней величины (для доли) по заданной вероятности;

2.  определение вероятности того, что расхождение между выборочной и генеральной характеристикой ,  не превзойдут определенную заданную величину;

3.  определение необходимой численности выборки, которая с определенной вероятностью обеспечит заданную точность показателя

·  Для повторного отбора

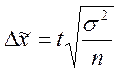
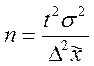
·  Для бесповторного отбора

.

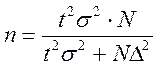            Распространение результатов выборки на генеральную совокупность.

Существует 2 способа распространения выборочных данных на генеральную совокупность:

1. способ прямого пересчета, т.е. средняя  умножается на численность совокупности;
2. метод поправочных коэффициентов, применяется в более сложных расчетах, когда выборочное наблюдение проводится с целью уточнения результатов сплошного наблюдения.

15. Понятие рядов динамики их виды. Показатели рядов динамики (абсолютные и относительные). Прогнозирование и экстраполяция в рядах динамики.

Под рядами динамики понимаются ряды статистических показателей, которые меняются во времени. Для рядов динамики используются следующие обозначения:

- временной показатель (годы, кварталы, месяцы, дни)

- уровень ряда, конкретное значение изучаемого показателя.

Ряды динамики бывают 2 видов:

1. Моментные показатели, т.е. значения приводят на определенный момент времени. Значения моментных рядов не складываются, т.к. каждое последнее значение может иметь предыдущее, что приводит к повторному счету;
2. Интервальные ряды, состоят из значений за более короткие промежутки времени (квартальные из месячных). Уровни интервального ряда можно складывать. 

Для анализа рядов динамики необходимо, чтобы данные были сопоставимы: во времени, по методикам расчета и в одинаковых ценах.

Показатели анализа рядов динамики.

Все показатели можно рассчитывать базисным способом, т.е. когда все уровни ряда сравниваются с уровнем, принятым за базу. Можно также использовать цепной способ, т.е. когда каждый уровень ряда сравнивается с предыдущим.

1.Абсолютный прирост  

       

2.Темпы роста  (доля, %)

   

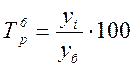
3.Темпы прироста  (доля, %)

    

4.Абсолютный прирост 1% прироста

        

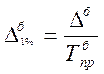
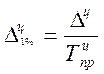
Прогнозирование и экстраполяция в рядах динамики.

Экстраполяция – распространение выявленных в анализе рядов динамики закономерностей на бедующее.

Основа прогнозирования – предположение, что закономерность, действующая внутри анализируемого ряда динамики выступает в качестве базы прогнозирования и сохраняется в дальнейшем.

16. Средние показатели в рядах динамики.

1.  Средний абсолютный прирост .

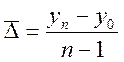, где

- последнее значение уровня ряда;

- первое значение уровня ряда;

- количество уровней.

  

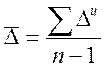
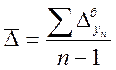
2.  Средний уровень ряда

·  Для интервальных рядов

- для равностоящих друг от друга уровней ;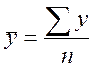

- для неравностоящих друг от друга уровней , где - промежуток времени между рядом стоящими уровнями.

·  Для моментных рядов

- когда равные промежутки времени между уровнями (ср. хронологическая)

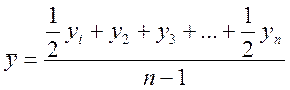  или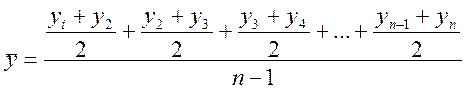

- когда промежутки времени не равны

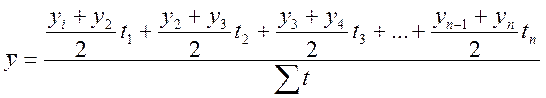, где - промежуток времени между двумя радом стоящими уровнями.

3.   Средний темп роста

·  для рядов, уровни которых идут друг за другом

, - количество темпов роста цепных;

·  для рядов, уровни которых имеют промежутки между собой

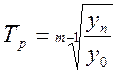, - количество лет между первым и последним уровнем ряда, если бы все значения шли последовательно.

4.  Средний темп прироста

     

17. Изучение основной тенденции развития (укрупнение уровней ряда, скользящая средняя, аналитическое выравнивание).

Для статистических расчетов, связанных с прогнозированием, необходимо знать тенденцию развития показателей в будущем.

Эту тенденцию можно определить следующими методами:

1. Укрупнение интервалов (месячные в квартальные, квартальные в годовые);
2. Метод скользящей средней. В основу метода положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция выражается в виде плавной линии. Для выявления тенденции устанавливаются звенья скользящей средней. Расчет скользящей средней определяется следующим образом:

, ;

3.  Аналитическое выравнивание – это выравнивание поло формулам.

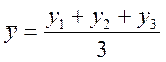- выравнивание по прямой  .

Для того, чтобы найти  и  воспользуемся методом наименьших квадратов: .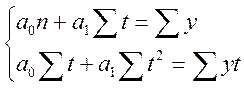

Для упрощения расчетов в статичстике используют следующий прием для нахождения  и :

• если количество уровней ряда четное

	t
1 год	-5
2	-3
3	-1
4	+1
5	+3
6	+5

                               

• если количество уровней ряда нечетное

	t
1 год	-2
2	-1
3	0
4	+1
5	+2

                .

,       .

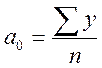
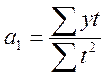18. Изучение сезонных колебаний.

Внутри годовые уровни многих показателей существенно зависят от сезонности (туризм, продажа сахара, сельское хозяйство, рыболовство, навигация). В таких случаях при укрупнении интервалов закономерность развития не только не проявляется, но и затушевывается. Поэтому изменение показателей в течении года анализируется при помощи индекса сезонности. В статистике существует 2 метода расчета индекса: