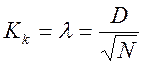 , где
, где ![]() -
максимальная разница по модулю между накопленными частотами двух распределений
(для
-
максимальная разница по модулю между накопленными частотами двух распределений
(для ![]() и
и ![]() ),
),
![]() - количество единиц в совокупности.
- количество единиц в совокупности.
![]() - чтобы гипотеза была не
опровергнута.
- чтобы гипотеза была не
опровергнута.
10. Понятие вариации. Абсолютные показатели вариации признака. Относительные показатели вариации признака.
Вариацией – называется отклонение каждого варианта x от его средней величины. Показатели вариации позволяют оценить однородность совокупности. Вариация оценивается при помощи абсолютных и относительных показателей.
Абсолютные показатели измеряются в тех же единицах, что и изучаемый вариант (x):
1.
Размах вариации ![]()
2.
Среднее линейное отклонение 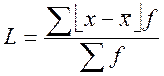 -
этот показатель показывает, насколько в среднем отклониться изучаемый вариант
от средней величины.
-
этот показатель показывает, насколько в среднем отклониться изучаемый вариант
от средней величины.
3.
Дисперсия 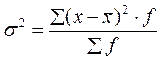 . Показатель
дисперсии маленькие расхождения между
. Показатель
дисперсии маленькие расхождения между ![]() и
и
![]() еще больше уменьшает, а большие
отклонения еще больше увеличивает.
еще больше уменьшает, а большие
отклонения еще больше увеличивает.
4.
Среднее квадратическое отклонение ![]() .
.
Относительные (доли, %):
1. Коэффициент
осцилляции 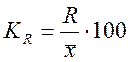 .
.
2. Коэффициент
линейного отклонения 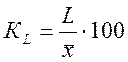 .
.
3. Коэффициент
вариации 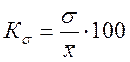 - именно этот показатель
показывает, однородна совокупность или нет. Если
- именно этот показатель
показывает, однородна совокупность или нет. Если ![]() или
33 %, то совокупность считается однородной.
или
33 %, то совокупность считается однородной.
11. Дисперсия. Свойства дисперсии. Порядок расчета. Правило сложения дисперсий. Дисперсия альтернативного признака.
Дисперсия 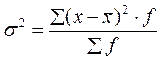 . Показатель дисперсии маленькие
расхождения между
. Показатель дисперсии маленькие
расхождения между ![]() и
и ![]() еще
больше уменьшает, а большие отклонения еще больше увеличивает.
еще
больше уменьшает, а большие отклонения еще больше увеличивает.
Свойства дисперсии.
1. если
все варианты значений ![]() увеличить или уменьшить на
увеличить или уменьшить на
![]() , то дисперсия не изменится.
, то дисперсия не изменится.
2. если
все варианты ![]() увеличить или уменьшить в
увеличить или уменьшить в ![]() раз, то дисперсия изменится в
раз, то дисперсия изменится в ![]() раз.
раз.
3. если
частоты увеличить или уменьшить на ![]() , то дисперсия не
изменится.
, то дисперсия не
изменится.
Дисперсия альтернативного признака.
Альтернативный признак – одни единицы обладают им , а другие нет.
Допустим ![]() =1-
обладает изучаемым признаком,
=1-
обладает изучаемым признаком, ![]() - не обладает.
- не обладает.
![]()
![]()
![]()
![]()
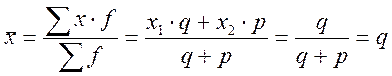
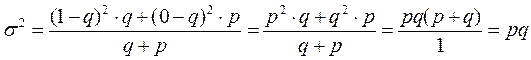 .
.
Правило сложения дисперсий.
Правила сложения необх. в тех случаях, когда изучаемая совокупность разделена на группы. В этом случае для нахождения дисперсии по всей совокупности можно воспользоваться правилом сложения дисперсий.
![]() ,
где
,
где
![]() -
общая дисперсия
-
общая дисперсия 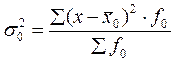 ,
, ![]() -
средняя величина во всей совокупности без деления на группы.
-
средняя величина во всей совокупности без деления на группы.
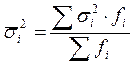 ,
где
,
где ![]() - дисперсия в каждой группе,
- дисперсия в каждой группе, ![]() - численность в каждой группе.
- численность в каждой группе.
![]() -
межгрупповая дисперсия
-
межгрупповая дисперсия 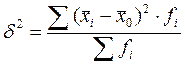 , где
, где ![]() - средняя величина в каждой группе.
- средняя величина в каждой группе.
Привило сложения дисперсий
позволяет выявить зависимость результатов от определяющих факторов при помощи коэффициента
детерминации – 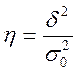 .
.
Межгрупповая
дисперсия ![]() дает обобщающую характеристику
случайных отклонений, возникающих под влиянием учтенного фактора, который
положен в основу группировки.
дает обобщающую характеристику
случайных отклонений, возникающих под влиянием учтенного фактора, который
положен в основу группировки.
12. Понятие выборочного наблюдения, области применения, способы отбора в выборочную совокупность. Собственно-случайная и механическая выборка. Определение предельной ошибки выборки для средней и доли при повторном и бесповторном отборе.
Под выборочным наблюдением понимается несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется случайно, отобранная часть подвергается обследованию, а результаты распространяются на всю совокупность.
В выборочном наблюдении используются следующие обозначения:
![]() - объем генеральной совокупности;
- объем генеральной совокупности;
![]() - объем выборочной совокупности;
- объем выборочной совокупности;
![]() - средняя величина генеральной
совокупности;
- средняя величина генеральной
совокупности;
![]() - средняя величина в выборочной
совокупности;
- средняя величина в выборочной
совокупности;
![]() - доля единиц, обладающих данным
признаком в генеральной совокупности;
- доля единиц, обладающих данным
признаком в генеральной совокупности;
![]() - доля единиц, обладающих данным
признаком в выборочной совокупности.
- доля единиц, обладающих данным
признаком в выборочной совокупности.
Целью
выборочного наблюдения является установка пределов, в которых будет
находится генеральная средняя ![]() или генеральная
доля
или генеральная
доля ![]() .
.
Единицы в выборочную совокупность могут отбираться двумя способами:
1. повторный – отобранные единицы после обследования вновь возвращаются в генеральную совокупность и могут быть обследованы вновь.
2. бесповторный.
Собственно-случайная выборка – каждая единица имеет одинаковую вероятность быть отобранной в выборочную совокупность.
· Для повторного отбора
- для средней 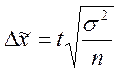
- для доли 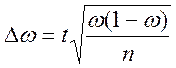
![]() - коэффициент доверия, зависит от
вероятности, с которой рассчитывается ошибка (табличное значение). При
вероятности:
- коэффициент доверия, зависит от
вероятности, с которой рассчитывается ошибка (табличное значение). При
вероятности:
![]()
![]() =1
=1
![]()
![]() =2
=2
![]()
![]() =3
=3
· Для бесповторного отбора
- для средней 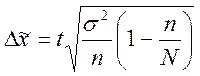
- для доли 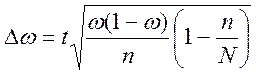 .
.
Механическая выборка – разновидность собственно-случайной. В этом случае генеральную совокупность делят на n равных количество групп, затем из каждой группы из середины выбирается по 1 единице, которые и подвергаются обследованию. Формулы для расчета предельной ошибки выборки такие же, как и для собственно-случайной.
Для того чтобы определить пределы, рассчитывают предельную ошибку выборки
![]() - предельная ошибка в выборке для
средней величины;
- предельная ошибка в выборке для
средней величины;
![]() - предельная ошибка в выборке для
доли.
- предельная ошибка в выборке для
доли.
Искомые границы будут определяться по формуле:
- для средней
величины ![]() или
или ![]() ;
;
- для доли ![]() или
или ![]() .
.
Расчет предельной ошибки в выборке зависит от вида выборки и способа отбора.
Предельная ошибка в выборке, рассчитывается двумя способами:
· Повторный
- для средней
величины 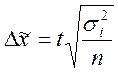
- для доли
единиц, обладающих данным признаком 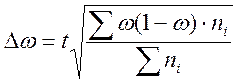 , где
, где ![]() - численность каждой группы.
- численность каждой группы.
· Бесповторный
- для средней
величины 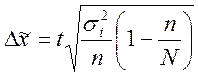
- для доли
единиц 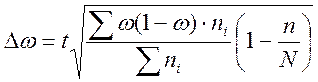
13. Типическая и серийная выборка. Определение предельной ошибки выборки для средней и доли при повторном и бесповторном отборе.
Типическая выборка – генеральная совокупность делится на однородные типические группы, затем из каждой типической группы собственно-случайным или механическим способом отбираются единицы в выборочную совокупность.
Серийная выборка – совокупность делится на однородные и одинаковые по объему группы – серии, внутри серии производится сплошное наблюдение единиц.
· Для повторного отбора
- для средней
величины 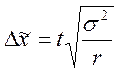
- для доли 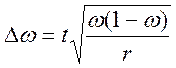
![]() - количество серий в выборке
- количество серий в выборке
· Для бесповторного отбора
- для средней 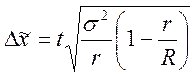
- для доли 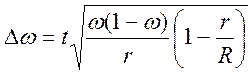 .
.
![]() - количество серий во всей
совокупности.
- количество серий во всей
совокупности.
Для того чтобы определить пределы, рассчитывают предельную ошибку выборки
![]() - предельная ошибка в выборке для
средней величины;
- предельная ошибка в выборке для
средней величины;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.