Методические указания к лабораторным работам "Определение коэффициента вязкости жидкости", "Определение молярной массы воздуха", "Определение удельной теплоёмкости металлов методом охлаждения", "Измерение относительной влажности воздуха", страница 7

С_тела = .

Эта величина измеряется в джоулях на кельвин (Дж/К) [1]. Теплоемкость весьма сложным образом может зависеть, в общем случае, от способа изменения температуры тела. Для газов, например, существенно, ведется ли нагревание (охлаждение) при постоянном объеме или при постоянном давлении [1]. Зависимость ее от температуры также сложна. Выбор конкретной физической модели, объясняющей ход зависимости С(T) может быть связан, кроме того, с родом материала (газ, твердое тело, жидкость), диапазоном температур и т.д. [2]. В частности, для металлов с простыми кристаллическими решетками и в определенном диапазоне температур (не слишком низких и не слишком высоких) достаточно хорошо «работает» теория Дебая. Однако к телам более сложной структуры формула Дебая не применима [3].

Очевидно, что получение значений теплоемкости при произвольной температуре для неизвестного материала является сложной и в то же время очень важной научно-технической задачей. В данной лабораторной работе используется оригинальный метод ее определения, предложенный сотрудниками НИИФ МГУ Я. А.Туровским и Г.М. Бартеневым в начале 40-х годов. Он был разработан для решения специальных задач, связанных с определением температурной зависимости теплоемкости металлов при высоких температурах [4][1].

Известно, что тело, нагретое до температуры выше температуры окружающей среды, со временем остывает, то есть, - отдает некоторое количество теплоты. Количество этого тепла, отданного за единицу времени, может быть выражено соотношением

,                                         (1)

где S - площадь поверхности тела, T_пов- температура поверхности тела; T_o - температура окружающей среды, a - коэффициент теплоотдачи[2].

Это же количество тепла может быть выражено через теплоемкость твердого тела:

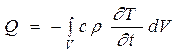,                                      (2)

где c - удельная теплоемкость материала (удельной теплоемкостью называется количество теплоты, которое необходимо сообщить единице массы тела, чтобы повысить ее температуру на один градус), r - плотность вещества, V - объем тела.

Согласно закону сохранения энергии мы можем приравнять правые части выражений (1) и (2), т.е.:

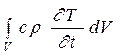
.                      (3)

Для дальнейших выкладок сделаем допущение, что теплоемкость и плотность вещества не зависят от объема, а коэффициент теплоотдачи постоянен по поверхности. Умножим и разделим левую часть равенства (3) на величину объема, а правую часть на величину поверхности. Тогда:

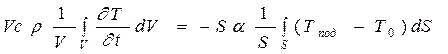.(4)

Величина 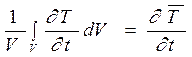 представляет собой среднее значение скорости охлаждения образца по объему V, а интеграл вида

-

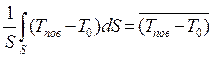среднее значение разности  по поверхности S. В соответствии с этим формулу (4) можно переписать в виде:

Vcr= - aS.(5)

При этом мы пренебрегаем малым изменением объема тела по сравнению с общим объемом тела в процессе охлаждения. Для эксперимента берутся два образца, изготовленные из различных материалов. В таком случае имеем следующую систему уравнений[3]:

V_Эc_Эr_Э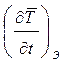 = - a_ЭS_Э

V_Хc_Хr_Х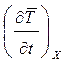 = - a_ХS_Х.                            (6)

При изготовлении с достаточной степенью точности обеспечена идентичность объемов, формы образцов и площади поверхности. То есть можно считать, что V_Э » V_Х, а S_Э» S_Х. Учитывая эту особенность, легко можно получить соотношение для искомой теплоемкости:

c_Х= c_Э 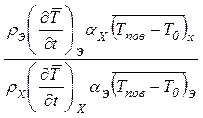.(7)

24

Как показывают оценки [4], для небольших образцов измерение температуры на поверхности можно заменить измерением температуры на оси образца. Если, кроме того, считать, что коэффициенты теплоотдачи исследуемого и эталонного образцов равны, и расчеты проводить для моментов времени, когда равны их температуры, то:

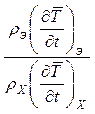c_Х = c_Э .                                              (8)

Величины r_Х, r_Эуказаны на установке, c_Э - выбирается на основании данных таблицы (Приложение № 2). Относительно последнего допущения (a_Х = a_Э) надо отметить, что оно может и не выполняться, поскольку коэффициент теплоотдачи является сложной функцией геометрических характеристик тела, температуры, скорости течения окружающего воздушного потока, плотности вещества и т.д. [7]. В данном опыте полностью устранить все указанные расхождения не удается.

Равенства коэффициентов теплоотдачи можно пытаться достичь путём специальной обработки обеих поверхностей (например, - хромируя их [4] непосредственно перед измерениями). Но такое покрытие также теряет свои свойства со временем, поэтому в условиях учебной лаборатории выполняемые расчеты носят оценочный характер.

Описание установки

 

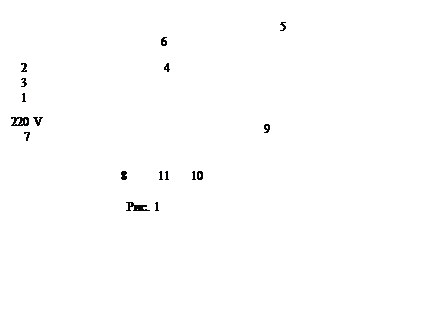Установка (рис. 1) состоит из корпуса 1, в котором закреплена цилиндрическая печка 2. В печку помещается нагреваемый образец 3, закрепляемый с помощью винтика, на фарфоровом стержне 4, через который пропущены концы термопары 5, (поскольку масса и размеры винтика значительно меньше массы и размеров образцов, то его влиянием на результаты эксперимента можно пренебречь). Концы термопары непосредственно подключаются к милливольтметру 6. Вилка, закрепленная на проводах, идущих от печки, включается непосредственно в сеть 7 с напряжением 220 В.

Корпус печки закреплён на направляющих рельсах 8. На этих рельсах установлен подвижный рейтер 9, на котором закреплен фарфоровый стержень с образцом. Рейтер фиксируется на рельсах винтом 10.

Порядок выполнения работы

Предварительные замечания. Так как на начальном этапе измерений температура образца спадает довольно быстро, то до включения установки следует заранее определить цену деления милливольтметра, заготовить таблицу 1, имеющую графы для занесения не менее 30 показаний; опробовать работу секундомера.

Снятие показаний целесообразно, по тем же причинам, делать вдвоем. Например, один студент диктует отсчет показаний термо-эдс в делениях шкалы милливольтметра, а второй делает отсчет времени и записывает оба показания в таблицу.

Внимание. Запрещается брать нагретый образец в руки и помещать любые предметы в отверстие печи.

1. Измерения. Для проведения измерений необходимо фарфоровый стержень с образцом 3 ввести в канал печки 2. С этой целью следует раскрепить винт 10, фиксирующий рейтер на рельсах и, перемещая его вдоль рельс, направить стержень с образцом в канал печки. После перемещения рейтера по рельсам 8 до упора 11 завернуть винт, фиксирующий рейтер 10. Контактные провода, идущие от термопары 5 необходимо подключить к милливольтметру 6. После этого включить в сеть кабель питания печки 7. Спустя некоторое время можно будет отметить рост показаний милливольтметра. Примерно через 15 - 20 минут они достигнут 9 - 10 мВ (порядка 200°С). В этот момент следует: