Методические указания к лабораторным работам "Определение коэффициента вязкости жидкости", "Определение молярной массы воздуха", "Определение удельной теплоёмкости металлов методом охлаждения", "Измерение относительной влажности воздуха", страница 5

Массу dm частиц газа, которым передан импульс поршнем, можно представить в следующем виде: dm =r×S×dl = rSu×dt (где r - плотность газа).

Это означает, что

 = r×S×u                                            (1)

Согласно второму закону Ньютона сила, действующая на газ со стороны поршня, равна скорости изменения его импульса:  F= dp/dt, причём

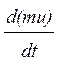 =  = m +  u.                                (2)   

Поскольку u= const, то   = 0; с учётом этого из (1) и (2) следует:

F = u =  u×r× S ×u,                                   (3)

где F - сила давления поршня.

Если учесть, что  эта сила связана с избыточным давлением Dp, которое создаётся поршнем, соотношением F =Dp×S, то из (3) получим:

Dр = r×u×u.                                                   (4)

Отметим, что здесь рассматривается случай небольших сжатий, и отличиями площади S поперечного сечения трубы и плотности r воздуха в «несжатой» и в «сжатой» областях можно пренебречь.

В случае объемной деформации газа формула закона Гука записывается следующим образом [3]:

Dр = - K× .                                              (5)

Здесь р - давление - аналог напряжения, K - модуль объемной упругости среды - аналог модуля Юнга, DV/V - относительная объемная деформация - аналог  относительного сжатия.

Объем газа, деформируемый за время Dt, легко подсчитать как:

V =u×S×Dt.                                                 (6)

Саму деформацию объема можно представить в виде

DV=- S×u×Dt.(7)

Знак «-» показывает, что при увеличении скорости поршня среда сжимается, а при уменьшении - расширяется.

Учитывая выражения (6) и (7), можно переписать формулу закона Гука:

Dр = K×.                                                  (8)

Теперь, используя выражение (4), из уравнения (8) получим, что скорость u_звука звуковой волны:

u_звука = .                                                (9)

Воспользовавшись формулой (5), приходим к выражению:

K = - V. При DV ® 0 это выражение можно переписать, как

DV®0

K = - V× lim = - V×.                               (10)

Поскольку V×r = m = const, то  = -. Следовательно,

К = r, а

u_звука = = 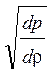.(11)

Ньютон предположил, что закон изменения давления и плотности газа в звуковой волне соответствует закону Бойля-Мариотта: выполняется условие = const. Исходя из этого, можно записать, что == сonst. Тогда

u_звука = .                                             (12)

Это и есть формула Ньютона.

Формулу Ньютона можно преобразовать, используя закон Клапейрона– Менделеева (выразив давление р газа через его плотность r):

р  =×r,

где R= 8,31 Дж/(моль×К) – универсальная газовая постоянная, m– молярная масса газа, Т – его температура. В результате получаем:

u_звука = 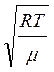.                                           (13)

Пользуясь этой формулой, можно вычислить, чему равна молярная масса воздуха m(если знать, чему равны u_звука, T и R). Однако, как показали дальнейшие исследования, различные области газа, по которому распространяется звуковая волна, имеют неодинаковую температуру (на это впервые указал П. Лаплас в 1816 году). Применим его подход к рассмотрению структуры звуковой волны.

Звуковая волна представляет собой чередующиеся в пространстве области разрежения и сжатия воздуха. Для сжатия воздуха внешние силы должны совершить работу над газом, в результате чего его температура в этой области будет несколько выше, чем в соседних. В разреженных же областях газ наоборот совершает работу и при этом охлаждается. Процесс сжатия-разрежения идет достаточно быстро, и температура не успевает выравниваться. Теплообменом можно пренебречь, поскольку теплопроводность воздуха в обычных условиях достаточно мала. Сказанное означает, что процесс сжатия-разрежения надо считать адиабатическим, а не изотермическим. Дифференцируя уравнение Пуассона для адиабатического процесса р×V^g= сonst, в котором g = С_p /С_V (отношение молярных теплоемкостей газа при постоянных давлении и объеме), можно записать:

dр×V ^g+g×р×V ^g-1×dV = 0, или

dр×V +g×р×dV = 0.                                        (14)

Если учесть, что r× V = const , то можно перейти к уравнению вида:

g×р×dr = r×dр, то есть

= g×.                                              (15)

Тогда, используя уравнение (15) и закон Клапейрона – Менделеева, формула для скорости звуковой волны в газе будет выглядеть так:

u_звука ==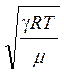.                                      (16)

Измерив температуру Т воздуха, и приняв во внимание, что его можно с хорошей точностью считать двухатомным идеальным газом, (в этом случае показатель степени в уравнении Пуассона легко рассчитывается теоретически: g  = 1,4), для определения mпо формуле (16) остаётся найти только скорость u_звука звуковой волны.

Методика измерений и описание установки

В данной работе реализован фазовый метод определения скорости звука, которая используется для дальнейших подсчетов молярной массы воздуха. Известно (см., например, [4]), что уравнение бегущей вдоль оси Х звуковой волны можно записать в виде:

р(x,t) = р₀×cos(wt - kx + j₀),                               (17)

где р(x,t) - давление в звуковой волне в зависимости от времени и координаты, w - циклическая частота, х - расстояние от источника до приемника звука, р₀ - амплитудное значение давления в волне, k -волновое число, j₀ - начальная фаза.

Если на пути звуковой волны поставить микрофон, то давление р, создаваемое звуковой волной, может быть преобразовано в электрическое напряжение U, снимаемое с микрофона (об устройстве микрофона рассказано, например, в [5]). Поскольку р ~ U, зависимость U(x, t) будет выражаться формулой, аналогичной (17):

U(x, t) = U₀×cos(wt - kx + j₀), или                           (18)

U(x, t) = U₀×cos(wt -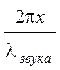 + j₀),

где U₀- амплитуда напряжения на микрофоне, l_звука - длина звуковой волны.

Подадим это напряжение на "Y" вход осциллографа, а на вход "X" - сигнал со звукового генератора, которым возбуждалась волна в источнике звука (динамик радиоприемника):