Физика \ Физика

Методические указания к лабораторным работам "Определение коэффициента вязкости жидкости", "Определение молярной массы воздуха", "Определение удельной теплоёмкости металлов методом охлаждения", "Измерение относительной влажности воздуха", страница 4

Для изохорического процесса при переходе газа из состояния 2 в состояние 3 имеем:

р2 / р3 = T2 / T1   .                                        (5)

Из уравнений (2) и (3) исключив Т2 / Т1, получим:

(р1 / р2)1 - g  = (р2 / р3)g.                                      (6)

После логарифмирования: (1 - g) (lg р1 - lg р2) =  g(lg р2 - lg р3),     или

g=(lg р1 -  lg р2)/ (lg р1 - lg р3 ).

Заменив р1, р2 и р3 на р1 = рА + Dр1,  р2 = рА,   р3 = рА+ Dр2 ,  получим:

g= [ lg(рA + D р1) - lg рA ] / lg(рA+ D р1) - lg(рA + D р2).

Учитывая, что  D lgx » Dx/x, если Dx малая по сравнению с x величина (Dр1 и Dр2малы по сравнению с рА), имеем:

g=Dр1 / (Dр1 - Dр2).

Принимая во внимание, что Dр =r gDh, где Dh - разница высот столбиков воды в манометре, окончательно получаем,

g=Dh1 / (Dh1 - Dh2) .                                       (7)

Порядок выполнения работы

В опыте исследуемым газом является воздух. В начале опыта при закрытом кране надо подкачивать воздух в баллон до тех пор пока разность уровней в коленах манометра не будет равна 25 - 30 см. Через некоторое время (около 2 – 3 минут), когда температура воздуха в баллоне сравняется с температурой окружающей среды, по манометру определяется избыточное давление Dр1  (Dh1пропорционально Dр1). Оно отсчитывается по разности уровней Dh1 в коленах манометра. Газ занимает состояние 1. Затем кран открывают, соединяя баллон с атмосферой и, дождавшись, когда воздух перестанет выходить из баллона, закрывают. (На установке с металлическим баллоном для выхода воздуха из баллона нажимают клапан, помеченный буквой К, а после выхода газа из баллона клапан отпускают).

Давление в баллоне упадет до атмосферного, и температура несколько понизится. Через некоторое время (около 2 – 3 минут) благодаря теплообмену температура в баллоне повышается до комнатной. В связи с этим давление в баллоне повысится и установится постоянным. В этот момент надо измерить разность уровней Dh2. Полученные показания Dh1и Dh2занести в таблицу. Весь опыт повторить десять раз.

Таблица

Измеряемые

и расчётные величины

Номер опыта

1

2

3

4

5

6

7

8

9

10

Dh1

Dh2

Dh1 - Dh2

12
 
g

Обработка результатов измерений

Вычислите g по формуле (5), после чего оцените среднее значение <g>:

<g> = (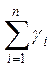)/n

и величину S

S = ,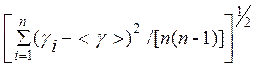

где n - число измерений.

Результаты вычислений представьте в виде:

g= <g> ± Sa

(здесь a- коэффициент Стьюдента). Значение доверительной вероятности выбрать равной 0,9.

Оцените относительную погрешность вычисления g:

dg=(Sa/<g>) ´100 %.

Значение <g> сравните с теоретическим, вычисленным по формуле (1), предполагая, что воздух является смесью двухатомных идеальных газов.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Запишите первый закон термодинамики.

2. Запишите формулу для расчета изменения внутренней энергии идеального газа.

3. Выведите выражения для молярной и удельной теплоемкости идеального газа при постоянном объеме и при постоянном давлении.

4. Рассчитайте молярные теплоемкости при постоянном объеме и при постоянном давлении для одноатомного и многоатомного идеальных газов.

5. Какой процесс называется адиабатическим? Что происходит с температурой газа при адиабатическом расширении и при адиабатическом сжатии и почему?

6. Объяснить различие между рассчитанными теоретически и полученными экспериментально значениями g.

7. Объясните, почему теплоемкость газа при постоянном давлении больше теплоемкости газа при постоянном объеме.

СПИСОК  ЛИТЕРАТУРЫ

1.  Савельев И.В. Курс общей физики, т. 1. М.: Наука, 1987, - 423 с.

2.  Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме / Н.А.Гринчар, Ф.П.Денисов, Б.А.Курбатов, В.А.Никитенко, А.П.Прунцев; Под общ. ред. Ф.П.Денисова. - М.: МИИТ, 1995. - с. 32.

РАБОТА №12

ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ВОЗДУХА

Цель работы. С помощью фазового метода определить скорость распространения звука в воздухе и его молярную массу.

Приборы и принадлежности. Излучатель звука (динамик), приемник звукового сигнала (микрофон), звуковой генератор, осциллограф, комплект проводов (перед использованием провода обязательно проверить).

Введение

Известно, что звуковая волна в воздухе – продольная, и представляет собой совокупность распространяющихся в пространстве чередующихся областей разряжения и сжатия воздуха. Именно на эти разряжения и сжатия реагирует, в частности, барабанная перепонка уха человека.

Впервые оценить скорость распространения звука, используя параметры газа, удалось Ньютону. Получим формулу Ньютона для скорости звука в газе [1, 2], положив для упрощения вывода, что звук распространяется в бесконечно длинной трубе с площадью поперечного сечения S, Пусть за время dt за счет движения поршня создано избыточное давление Dp на фоне давления p, при котором находится газ в трубе. При этом какому-то слою воздуха массой dm передан импульс. За это время поршень сместится на некоторое расстояние dl и по трубе пойдет волна сжатия, которая за время dt распространится на расстояние dL(рис.1).

Таким образом, скорость волны равна u= dL/dt. Однако, сами частицы во всем слое длиной dl будут двигаться со скоростью u = dl/dt, что соответствует скорости движения самого поршня. Поскольку поршень движется равномерно, то u=const.

Скачать файл