Методические указания к лабораторным работам по дисциплине «Контактная сеть», страница 8

            а – расстояние от оси опоры до точки крепления рессорного троса, [м].

                                                                                 ,                                                                                  

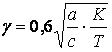где с – расстояние от оси опоры до первой нерессорной струны, [м].

Эластичность рессорной подвески в точке 1 (Зона Б):

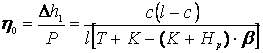                                        ;                                                 (2.9)

                                                            .

Формула (2.9) может быть использована и для определения коэффициента эластичности нерессорной цепной подвески в зонах А и Б. При этом расстояние от оси опоры до точки крепления рессорного троса принимается равным нулю.

На рис.2.3 приведены эпюры эластичности для простой и цепной контактных подвесок.

 

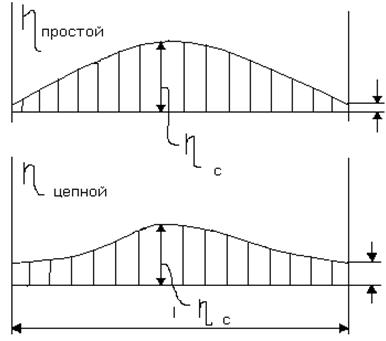
Рис.2.3. Эпюры эластичности: а) для простой подвески,
б) для цепной подвески

Неравномерность эластичности в пролёте характеризуется отношением минимальной её величины к максимальной

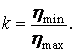                                                                                                                                                                        (2.8)

У лучших контактных подвесок этот показатель близок к единице.

Описание стенда

На стенде смонтированы цепная рессорная подвеска и цепная нерессорная подвеска. На столах уложены модели рельсов, по которым могут перемещаться тележки с токоприёмниками. Высота расположения проводов и точек контакта измеряется линейкой от поверхности стола.

Содержание работы

Исследуют взаимодействие цепной рессорной и нерессорной подвесок с токоприёмником. Измеряют высотное положение контактного провода для обеих подвесок и вычерчивают кривые его провисания. Замеряют подъёмы провода и строят траектории движения токоприемника. Строят эпюры эластичности. Сравнивают опытные и расчётные данные, коэффициенты эластичности подвесок.