Методические указания к лабораторным работам по дисциплине «Контактная сеть», страница 7

Эластичность провода

                                                                                                                                              (2.4)

Уравнение траектории движения точки контакта

                                                                                                          (2.5)

Из выражения (2.5) можно заметить, что при  , и, следовательно, траектория будет прямолинейной.

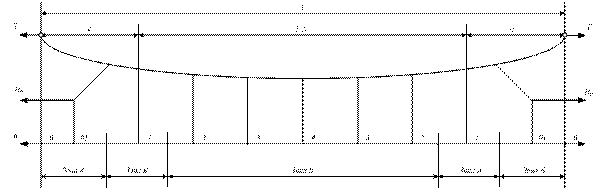Рис. 2.2. Схема цепной рессорной контактной подвески

Подъём контактного провода, эластичность, траектория движения токоприёмника при цепных подвесках зависят от их конструкции. Из-за особенностей конструкции опорного узла расчет по одним и тем же формулам в различных частях пролета затруднен. Поэтому в рессорной контактной подвеске обычно выделяют три расчетные зоны (рис. 2.2). В средней части пролета (Зона В) одинарной цепной рессорной и нерессорной подвесок для определения подъема контактного провода  при расположении силы P под струной может быть использована формула:  

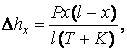                                                                                                                                                      (2.6)

где T – натяжение несущего троса, [даН];

            K – натяжение контактного провода, [даН].

Эластичность цепной подвески

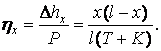                                                                                                                                            (2.7)

Эластичность цепной рессорной подвески в точках 0 и 0^/ (Зона А) может быть определена по формулам:

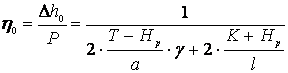                                 ,                                           (2.8)

где  – натяжение рессорного троса, [даН];